호떡의 개발일기

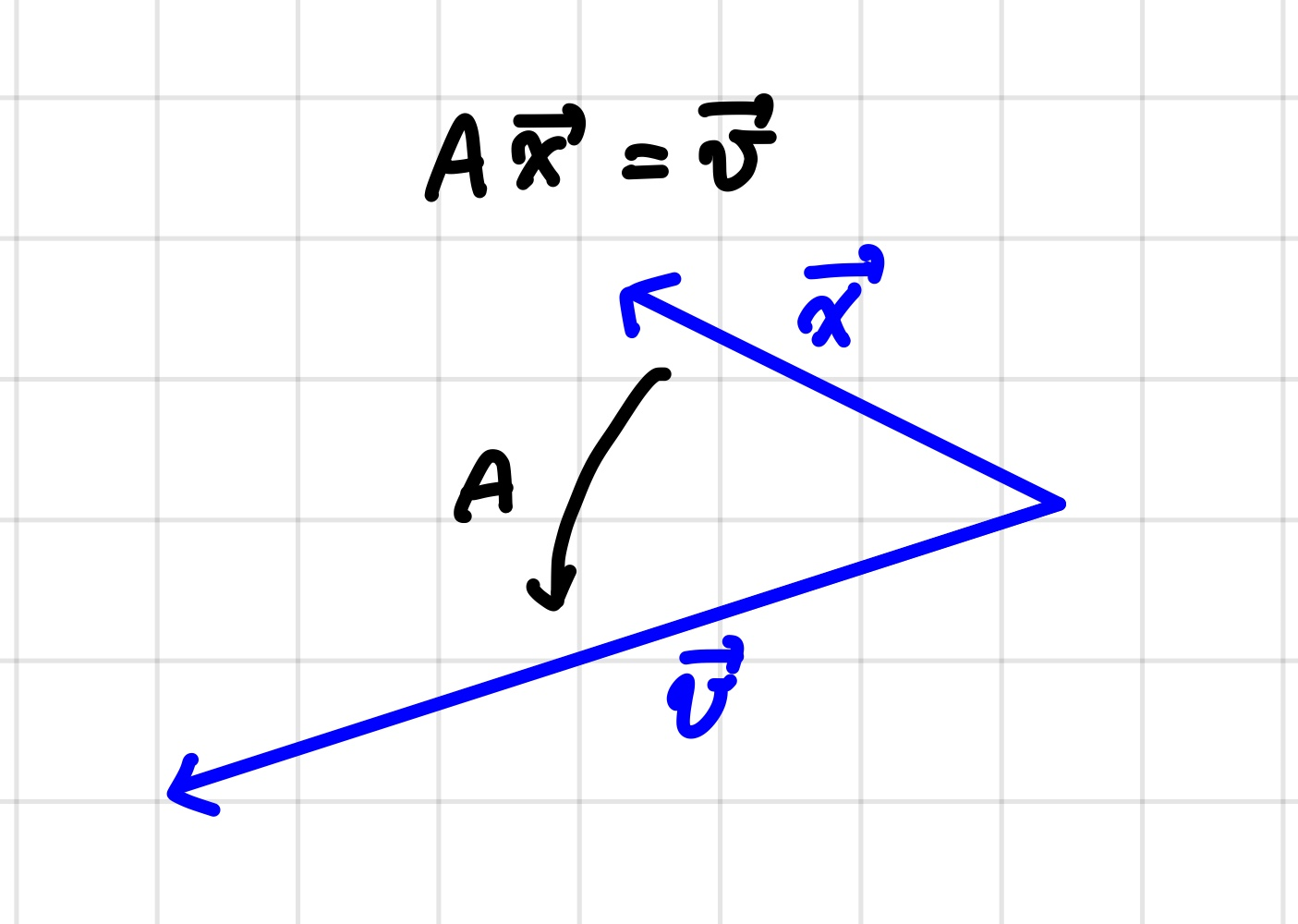
출처 : 

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 

안녕하세요

호떡입니다.

바로 시작해볼까요~?

--------------------------------------------------------------------------------------------------------------------------------------

오늘은 "좌표계"의 기저벡터의 변환과 적용에 대해 알아볼 것입니다. 

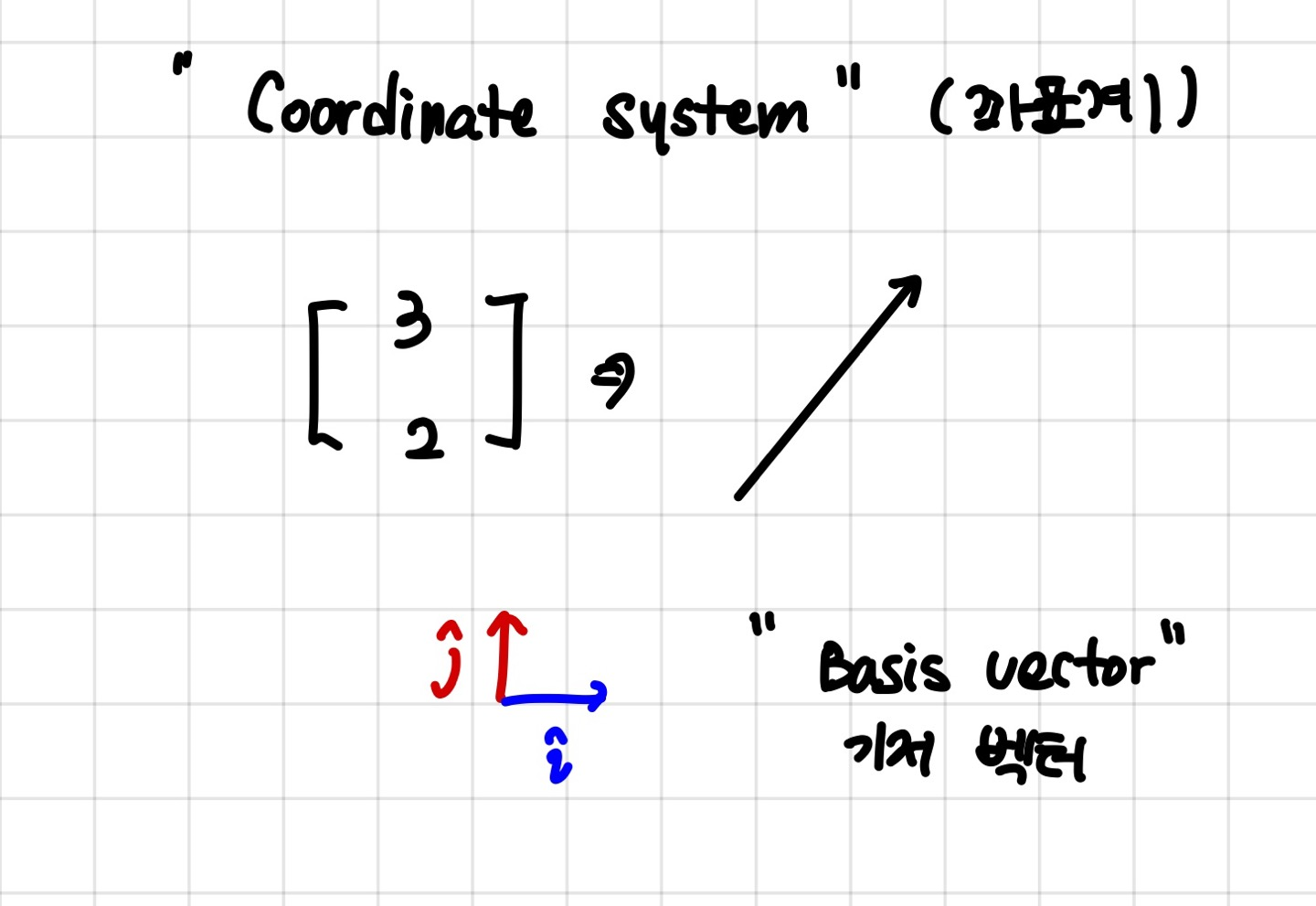
벡터 3,2 를 생각해보죠.

우리는 3,2를 Basis vector, 기저벡터로 나타낼 수 있습니다.

바로 

3i + 2j 처럼 말이죠.

좌표계 뒷면에 그려지는 Grid는 (저는 복잡해서 못그렸지만 .. ㅠㅠ) 시각적 도움에 불과합니다.

하지만, 어떻게 그리던 원점은 같습니다. 

이때 원점은, 어떤 벡터를 가지고 있던 크기를 0으로 줄였을 때 의미하는 곳 입니다. 

우리가 일반적인 좌표계에서 가지고 있는 기저벡터 i,j 자체를 다른 벡터로 정하면 어떨까요?

우리 좌표계의 basis vector를 바꿔보는 거죠!

바뀐 basis vector의 세계를, 제니퍼의 관점으로 묘사해보도록 하겠습니다. 

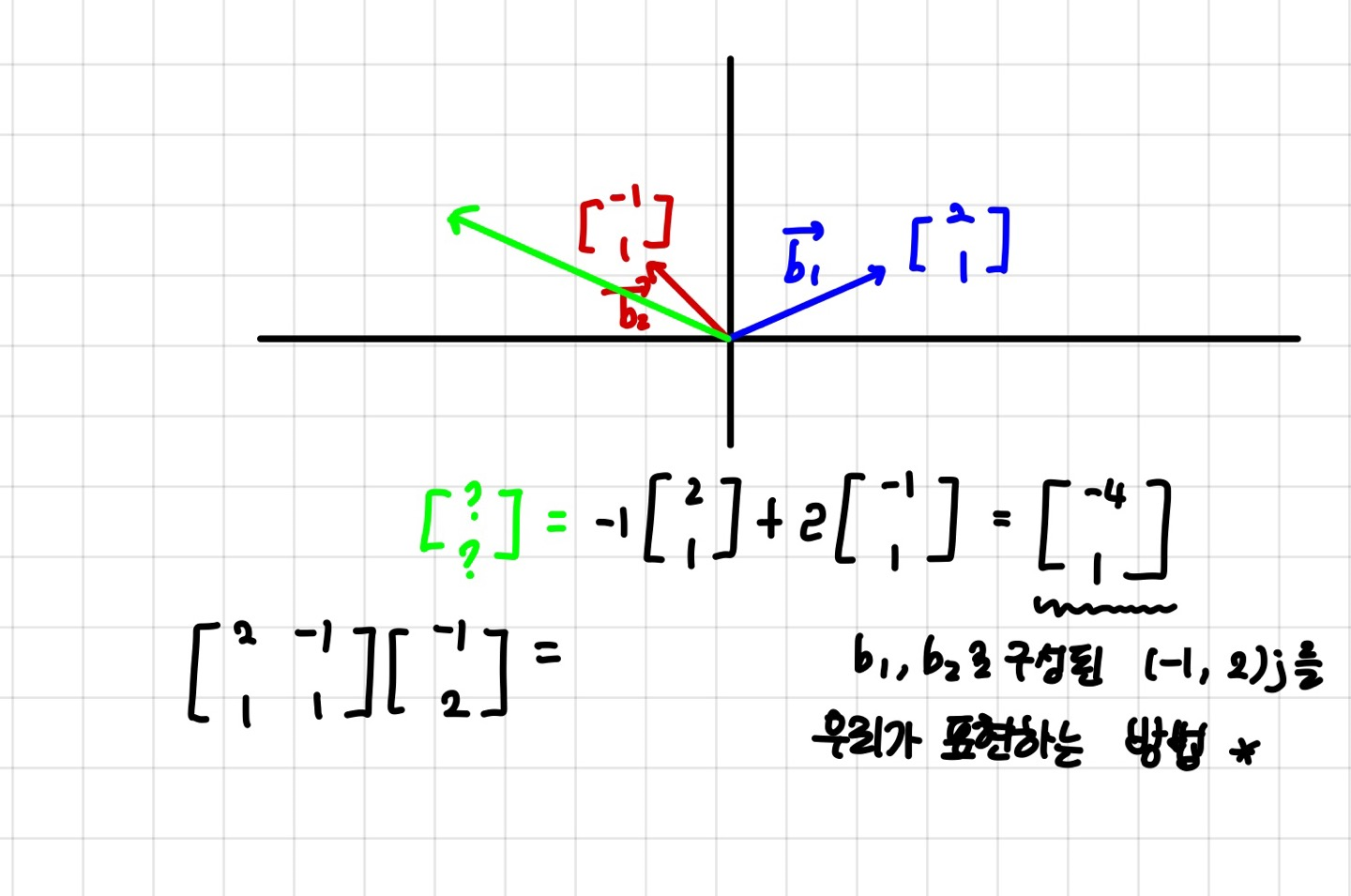
만약 제니퍼는 b1, b2를 기저벡터로 정의하였다고 합시다. 

제니퍼가 자신의 관점에서 (-1,2)벡터 (초록색)을 그렸다고 할때, 우리의 좌표계에서는 -1,2가 어떻게 바뀔까요??

바로 선형변환의 식을 통해 구할 수 있습니다. 

제니퍼의 관점인 -1,2에, 제니퍼의 기저벡터를 변환 행렬로 생각하면 됩니다.

우리에게는 -4,1이 되는거죠.

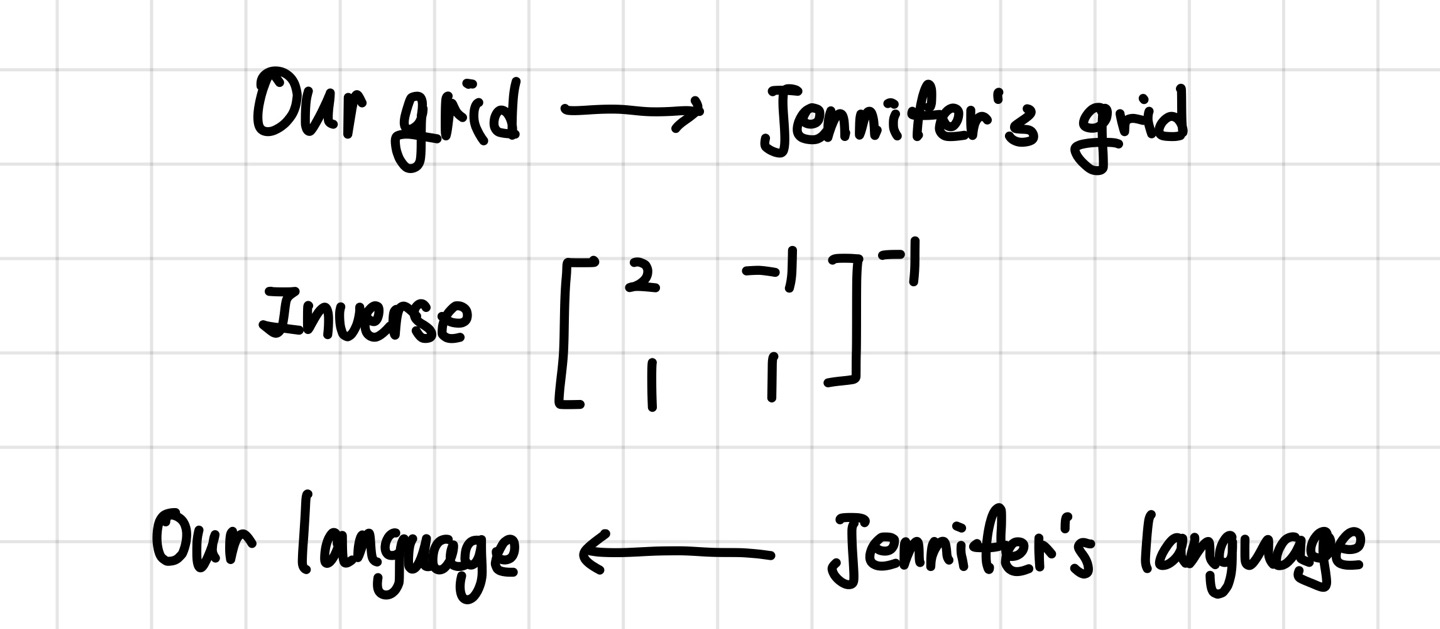
우리의 Grid를 제니퍼의 grid 버전으로 바뀔 수도 있고,

그 반대도 됩니다.

이때 , 앞서와 반대로 변환해주고자 한다면 행렬의 역행렬을 곱해주기만 하면 됩니다. 

우리의 grid에서 정의된 3,2 를 그녀의 grid상에서 표시하려면,

우리는 역행렬을 곱해주기만 하면 됩니다.

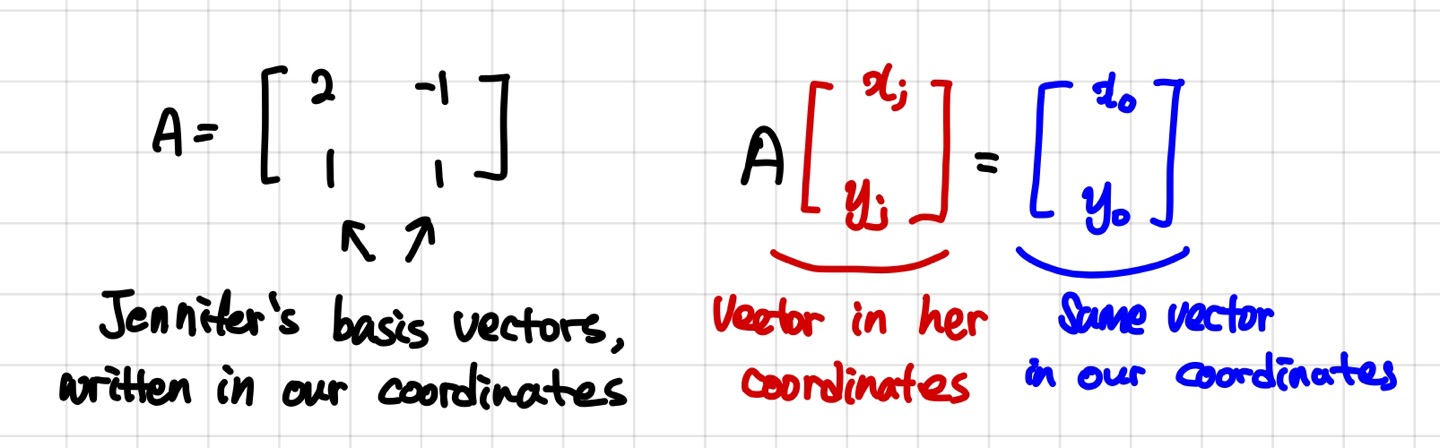
제니퍼의 기저벡터는 선형변환 행렬이되어

제니퍼에서 정의된 x,y에 이 행렬을 곱하기만 하면

우리좌표계에서 같은 곳을 나타내는 벡터를 찾는게 가능합니다.

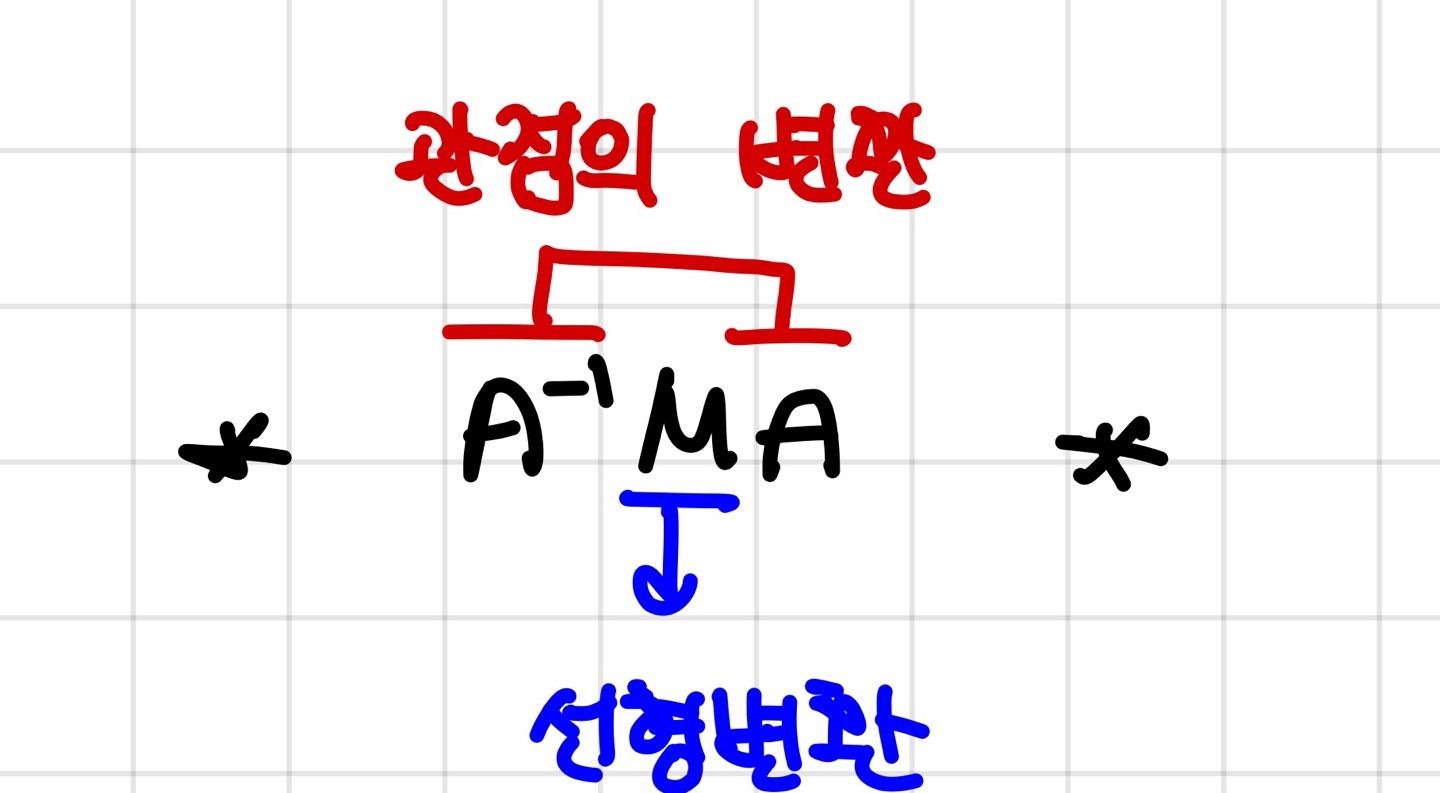
그러면 여러분들이 선형대수를 공부할때 많이 봤을 이 식을 이해할 수 있습니다!

천천히 생각해볼까요?

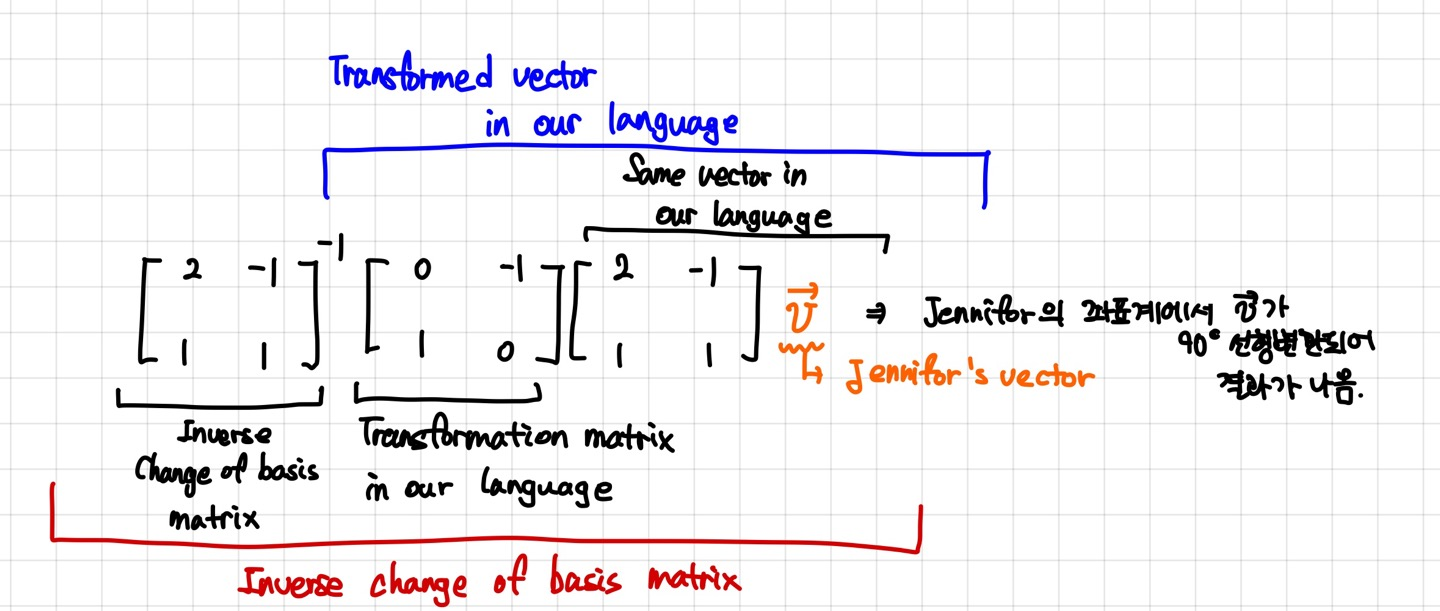
만약 90도 rotation하는 선형변환 식인 [[ 0 -1 ][ 1 0 ]]을 적용한다고 해보죠.

이때, 이 선형변환 식은 우리 좌표계에서만 90도 회전인 식이죠.

제니퍼의 그리드에 이것을 적용하면 대부분의 경우 90도 회전이 나오지 않습니다.

그렇죠?

하지만 제니퍼의 벡터에 제니퍼의 기저벡터 행렬을 곱해주면, 우리 grid에서 표현할 수 있게됩니다.

그러면 우리의 관점으로 바꿔지게 되고, 여기에는 90도 rotation 선형변환 행렬을 곱할 수 있게되죠.

하지만!

우리는 제니퍼의 그리드에 적용하고 싶은 거잖아요?

결국엔 역으로 다시 제니퍼 기저벡터의 역행렬을 곱해주면,

제니퍼의 그리드에서 90도 회전을 적용할 수 있는거죠.

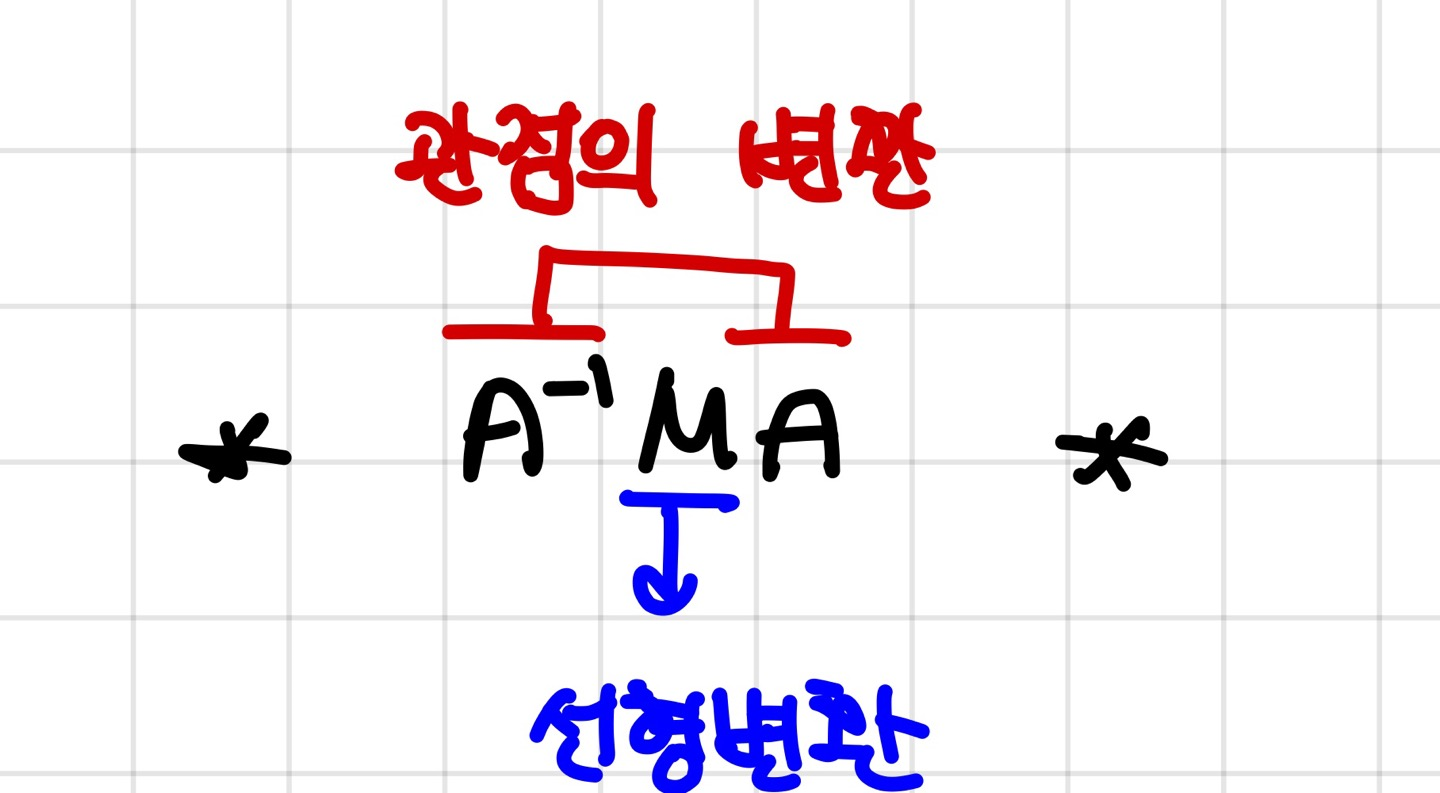
그럼 이제 이식이 이해 되셨을 것이라 생각합니다. 

그럼 뿅~

출처:

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab] 

안녕하세요

호떡입니다.

오늘은 꽤나 중요한 개념인 역행렬, 영공간, 열공간에 대해 알아보겠습니다.

바로 시작해봅시당

------------------------------------------------------------------------------------------------------------------------------

1] Inverse matrices

2] Column Space

3] Rank

4] Null Space

먼저 배워보기 전에 Linear system of equations (선형 방정식계) 에 대해 살펴봅시다.

우리는 변환 후 행렬 벡터 A(상수, Coefficient)를 통해 변환 후 벡터 v를 알 수 있다고 배웠습니다.

그럼 여기서, A를 어떻게 구할까요? 

결국 원래의 x벡터가 v벡터로 변하는거니, 두가지 아이디어를 낼 수 있습니다.

1] 공간을 축소시키는 경우 (det A = 0)

2] 공간을 축소시키지 않고 동일한 경우 (det A != 0)

먼저 2의 경우부터 봅시다.

detA != 0 이라는 것은 행렬 A가 같은 방향의 기저벡터가 아닌 확장된 span으로서의 영역을 의미합니다.

위의 그림에서 x가 A의 곱을 통해 v가 된것처럼, 반대로 v에서 A의 역을 곱해 x가 될 수 있습니다.

양변에 A의 역행렬을 곱해준뒤 A-1A = I가 되고, 이전벡터 x를 구할 수 있게 됩니다.

그럼 1의 경우를 살펴봅시다.

1의 공간을 축소시키는 경우는 det A=0, 즉 면적이 0팩터로 확장, 없어지는 것이기 때문에 같은 직선 상에서 스케일링만 되었다고 생각할 수 있습니다.

그렇다면, 뭉개진 선을 되돌려서 평면으로 만들 수 없겠지요.

바로 여기서, Rank의 개념이 등장합니다.

공간변환의 결과가 선(line)이라면, 즉 1차원이라면 Rank(A) = 1

2차원이라면, Rank(A)=2

Rank란, 변환 결과의 차원 수를 의미합니다.

그럼 여기서 질문!!

2차원 공간상에서 Rank(A)가 2일때, detA 의 값은 무엇일까요?

바로 detA != 0이 됩니다.

2차원 공간상에서 공간변환의 결과가 2차원이기 때문에, determinant는 평행사변형의 면적이 되는 것이죠.

즉, Full Rank상태가 됩니다.

그럼 3차원일때, Rank(A) = 2라면 무엇을 뜻하는 걸까요?

공간이 Collapse(축소)했음을 뜻합니다.

하지만, Rank(A) = 1만큼 붕괴된 것은 아니죠.

여기까지는 다들 이해되셨죠 ?

이어서,

행렬의 가능한 결과의 집합을 선이든, 평면이든, 3차원 공간이든지 간에 우리는 열공간이라고 부릅니다.

Zero vector(영벡터)는 어느 열공간에든지 포함됩니다.

왜냐하면, 선형변환에서는 반드시 원점이 고정되어야 하기 때문이죠.

원점으로 이동하는 벡터들의 집합을 그 행렬의 영공간(null space) or 커널(Kernel)이라고 부르게 됩니다.

오늘의 포스팅은 여기까지~!

출처:

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab

안녕하세요

호떡입니다

오늘은 선형변환과 행렬에 대해 알아보겠습니다.

우리가 항상 자동적으로 생각하고 계산했던 행렬과 벡터의 곱셈에 대한 본질적인 이해를 해보려 합니다.

그럼 Start~~!!

-----------------------------------------------------------------------------------------------------------------------------------------------------------------

1. Linear Transformation (선형변환)이란? 

우선 단어대로 한번 생각해보자

선형 (Linear) + 변환 (Transforamation)

선형은 알겠고,

그럼 여기서, 변환은 무엇을 뜻할까?

먼저, 변환을 함수의 개념으로 접근해보자

함수는 무엇인가?

위의 그림은 함수를 나타내며, 함수는 input을 Output으로 변환해주는 역할을 한다.

즉, Transform == function으로 이해할 수 있다. 

그럼 이제 선형의 속성을 알아보자.

Transfer, 즉 function이 선형적(Linear) 이라는 것은 두 가지 속성을 의미한다.

1] 모든 선들은 변환 이후에도 휘지 않고 직선

2] 원점은 변환 이후에도 여전히 원점

Grid lines remain parallel and evenly spaced == 그리드 선은 평행하고 균일한 간격을 유지합니다.

이 두가지 조건만 지킨다면, 선형 변환이라고 할 수 있다. 

예시로, (-1,2)의 v벡터를 생각해보자.

위의 그림을 보면, v벡터는 2차원의 기저벡터 i와 j의 스케일링되고 합해진 선형조합이다.

여기서 v를 선형 변환하게 되면

변환 후에도 같은 선형결합을 유지하게 된다. 

그럼 여기서 나의 목적은 무엇일까?

변환 후 벡터 v를 알고 싶은 것이다. 

그럼 변환 후 v는 어떻게 구할까?

바로, 변환후 기저벡터 i와 j를 알면 변환함수 f(x)를 구할 수 있다. 즉, f(x)를 알게된다면 변환 후의 v벡터를 알 수 있다. 

변환 후 좌표를 x와 y로 생각하고 정리해보자.  

위의 그림처럼 변환 후 벡터 i와 j를 알 수 있다면, x와 y벡터는 변환 전 i와 j벡터의 선형조합으로 표현되므로 최종적으로 변환 후 좌표 x와 y를 구할 수 있다.

위의 그림에서, 변환 후 벡터를 2X2 matrix로 표현 가능하다.

왼쪽 열은 변환후 i벡터, 오른쪽 열은 변환 후 j벡터이다.

궁금한 벡터가 (5, 7)이라고 했을 때, 변환 후 벡터 i와 j를 알고 있다면 우리가 익히 알던 행렬 벡터 곱셈을 통해 변환 후 좌표를 알 수 있다.

즉 변환 후 새 기저 벡터들로 스케일링하고 합한다는 개념이 된다.

우리가 익히 알고있는 행렬 벡터 곱셈이다.

행렬 벡터 곱셈은, 내가 원하는 벡터를 어떤 함수를 통해 변환하여 공간변환된 상태에서의 벡터를 구하는 것이다.

그러면 행렬을 공간의 변환으로 생각해도 되는걸까?

정답은 ..

맞다.

2차원이라고 가정했을 경우 그 공간의 basis벡터인 i와 j가 공간의 변환의 적용을 받고, 적용 받은 후의 i와 j가 행렬로 표현되는 것이다. 

오늘의 포스팅 끝~! 

어쩌다 보니 몰아서 쓰고있는데...  다음부터는 꾸준히 써야지 ㅠ