출처:
https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
Essence of linear algebra
A geometric understanding of matrices, determinants, eigen-stuffs and more.
www.youtube.com
안녕하세요
호떡입니다.
오늘은 비정사각형 행렬에 대한 이해를 해보려합니다.
그럼 start~~~~~~~!!!!!
--------------------------------------------------------------------------------------
이전까지의 포스팅에서는 항상 정사각형 행렬만 다뤘었죠
뭔가 이상하지 않나요?
선형대수학을 배웠을 땐 분명히 여러 shape의 행렬을 다뤘던 것 같은데 말이죠..
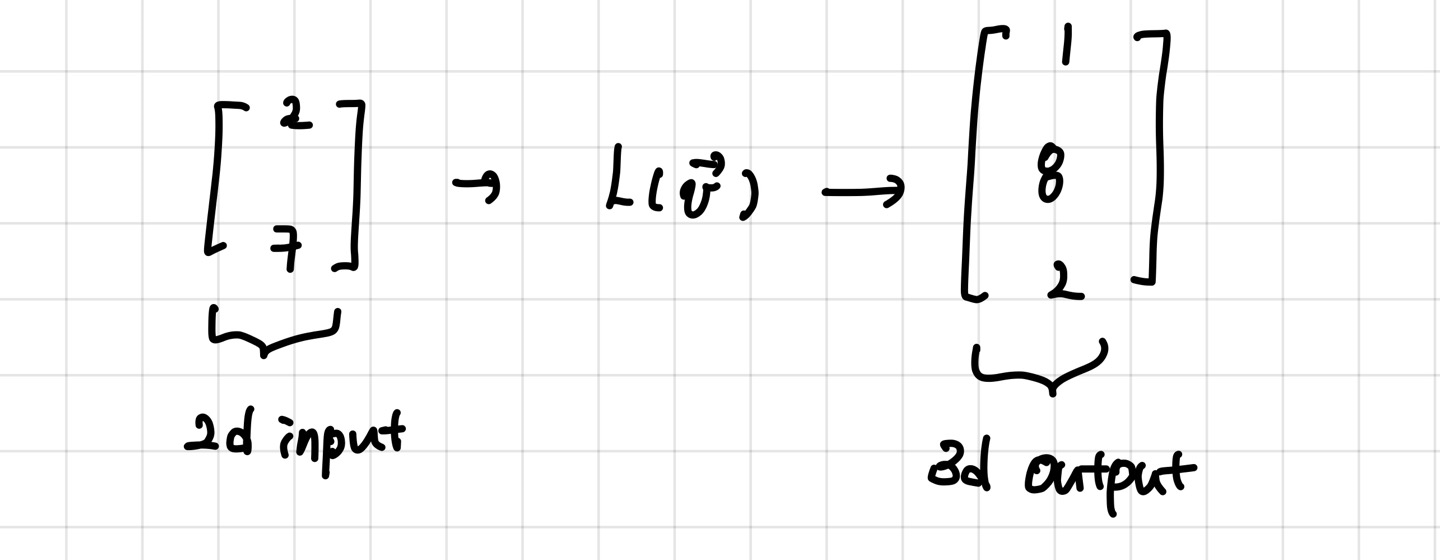
그냥 단순하게 생각해봅시다.
2차원의 input이, L함수의 선형변환을 통해 3차원의 Output이 되었다고 생각해보면
변환 후 기저벡터들은 어떻게 쓸 수 있을까요???

다음과 같은 형태로 표현할 수 있겠죠.
분명히 열이 2개인 것으로 보아 변환전엔 i와 j밖에 없었는데, 변환 후 i벡터는 3차원이 됩니다.(행의 개수 3개)
신기하죠?
기하학적으로 2차원 공간을 3차원 공간으로 확장한 셈이 됩니다.

(1,0)이었던 i벡터는 2,-1,-2가 되고
(0,1)이었던 j벡터는 (0,1,1)이 됩니다.
행렬식을 보니 이해가 쉬워지죠.
그럼 여기서 질문!
3*2행렬은 어떤 의미일까요?
바로 공간의 축소를 뜻합니다.

3개의 basis vector가 있었지만, 결론적으로 나중엔 2차원 벡터로 변환됩니다.
즉, 3차원 -> 2차원의 공간 축소라고 볼 수 있겠죠!
이해되셨나요~?
그럼 오늘의 포스팅 진짜 끝~~!!
'Linear algebra' 카테고리의 다른 글
| [Linear algebra] Chapter10: Cross Product (0) | 2022.07.06 |
|---|---|
| [Linear algebra] Chapter9: Dot products and duality (0) | 2022.07.05 |
| [Linear algebra] Chapter7: Inverse matrices, column space and null space (0) | 2022.07.04 |
| [Linear algebra] Chapter6: The determinant (0) | 2022.07.04 |
| [Linear algebra] Chapter5: Three dimensional Linear Transforms (0) | 2022.07.04 |