호떡의 개발일기

- SSH 접속

쉘 창에 => ssh 계정@IP

ex) ssh hj@168.~~

- VNC 접속

1. TigerVNC viewer설치

VNC server 창에 IP:5900+X(포트번호) 입력하여 Connect

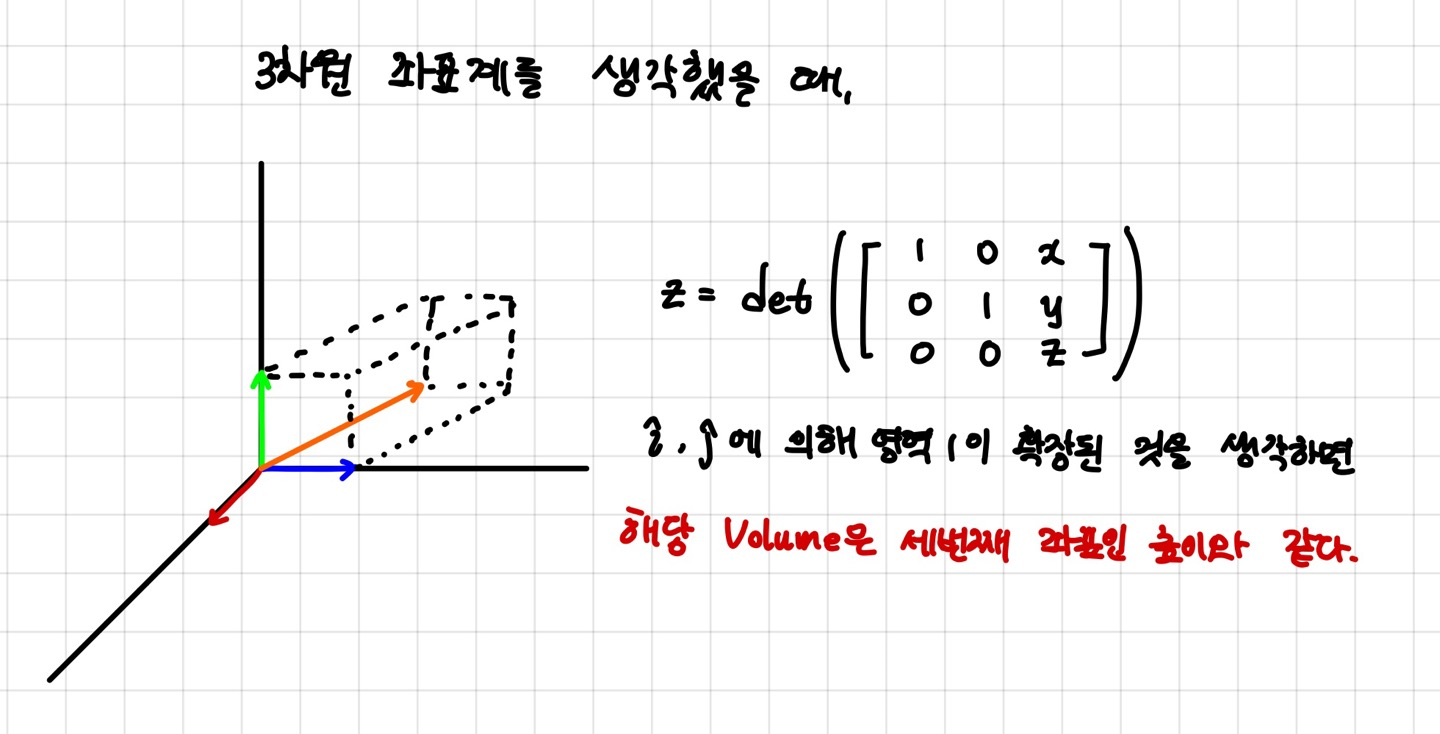
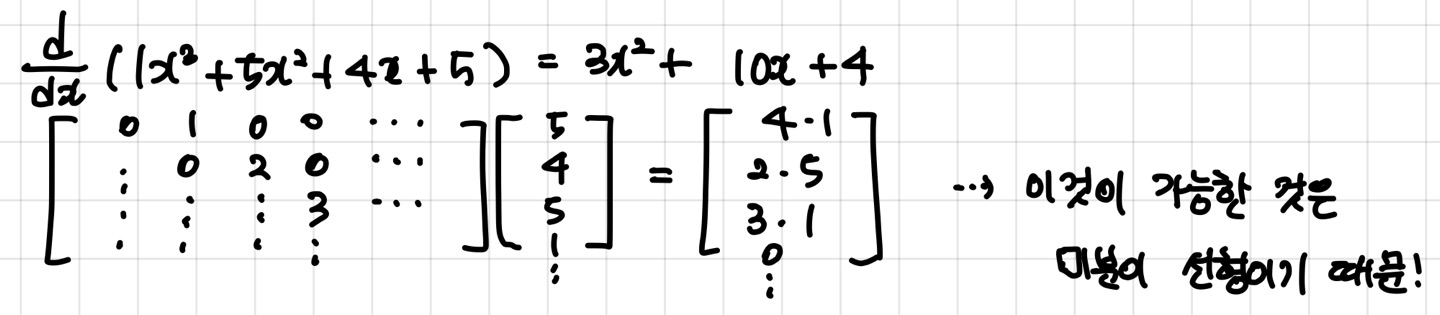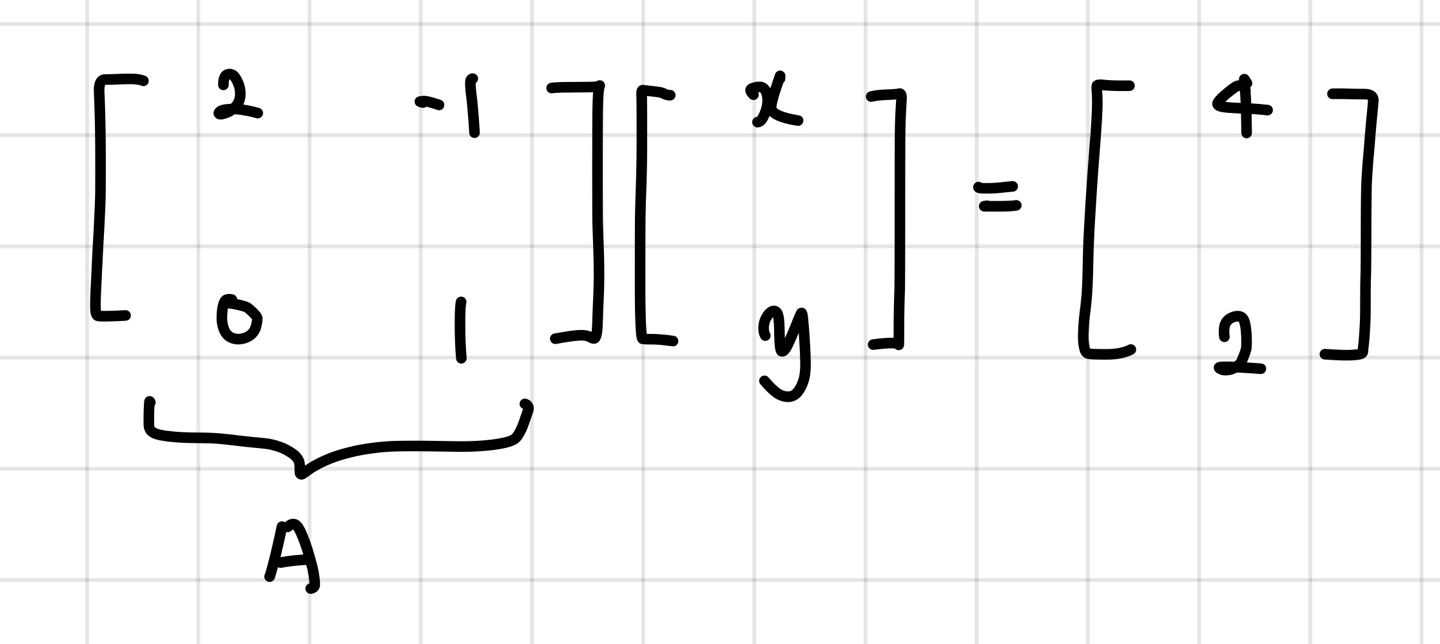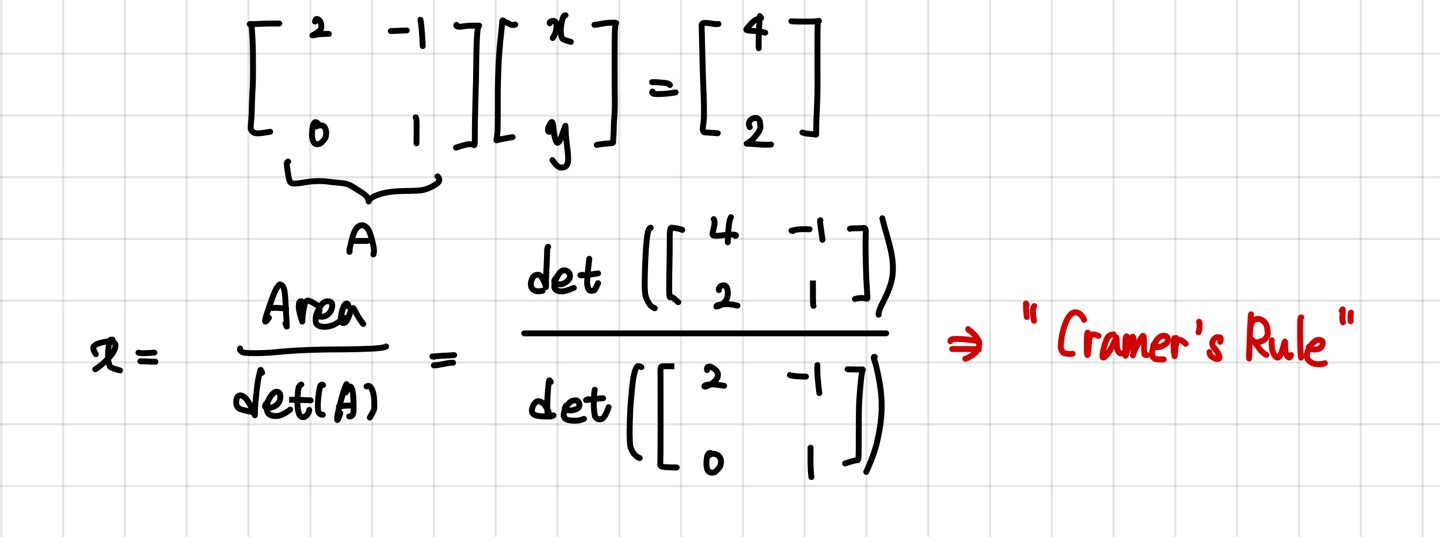출처:

https://www.youtube.com/watch?v=8idr1WZ1A7Q&t=5s 

안녕하세요

호떡입니다.

좋은 오후네요.

오늘 자랑 하나 하자면,,

잠을 12시간이나 잤습니다!

오히려 잠을 더 자니 멍한 기운이 드는 군요. 

다들 기운 차리시고 오늘의 포스팅 시작하도록 하겠습니다.

-----------------------------------------------------------------------------------------------------------------------------------------------------------------

Probabilities of probabilities Part 1.

여러분은 이번에 휴대폰을 사려고 합니다.

아이폰 13 mini, 아이폰 13, 아이폰 13 pro 중에 고민중이죠.

그리고 각각 제품의 후기를 보게 됩니다.

아이폰 13 mini의 후기는 10개의, 100%의 만족률이었습니다.

아이폰 13은 50개의 리뷰, 96%의 만족률이죠.

아이폰 13 pro 는 200개의 리뷰, 93%의 만족률이었습니다.

그럼 여러분은 단순히 리뷰만 가지고 어떤 것을 사야할지 판단할때, 

무엇을 사야 할까요?

확률로만 따지자면 아이폰 13미니를 사는게 최선의 방법일 겁니다. (사실 제 폰이 아이폰 13 mini ㅎㅎ)

그렇지만, 10건의 리뷰밖에 존재하지 않죠.

내가 저 물건을 샀을 때, 만족할 확률을 알아야하는데..

이는 어떻게 알 수 있을 까요?

바로

리뷰가 더 있는듯 생각하면 됩니다.

예를들어 리뷰가 2개 더 있다고 생각해보죠.

그리고 하나는 만족, 하나는 불만족이라고 가정합니다.

아래 그림처럼 말이죠.

원래는 10개중에 10개의 리뷰 모두 100%였다면, 

여기서는 12개의 리뷰가 있고 1개의 리뷰가 불만족이니

총확률은 11/12 = 91.7%가 됩니다.

이런식으로 모두 계산해보면,

아이폰 13 mini ==> 91.7% (내가 샀을 때 만족할 확률)

아이폰 13 ==> 49/52 == 94.2%

아이폰 13 pro ==> 187/202 = 92.5%

즉, 내가 샀을 때 만족도가 제일 높은 제품은 아이폰 13입니다!

이런식으로 계산하는 것을 라플라스의 성공법칙이라고 하죠.

자, 그럼 다른 경우를 생각해봅시다. 

만족할 확률 s=0.95 가 주어졌을 때,

48개의 리뷰가 만족이고, 2건의 리뷰가 불만족일 확률은 어떻게 될까요?

여러 번의 시뮬레이션을 돌려보고, 아래와 같은 분포가 나왔다고 가정해보죠.

바로 확률의 확률입니다.

만족할 확률이 주어졌을 때, 해당 확률(데이터)가 나올 확률이죠.

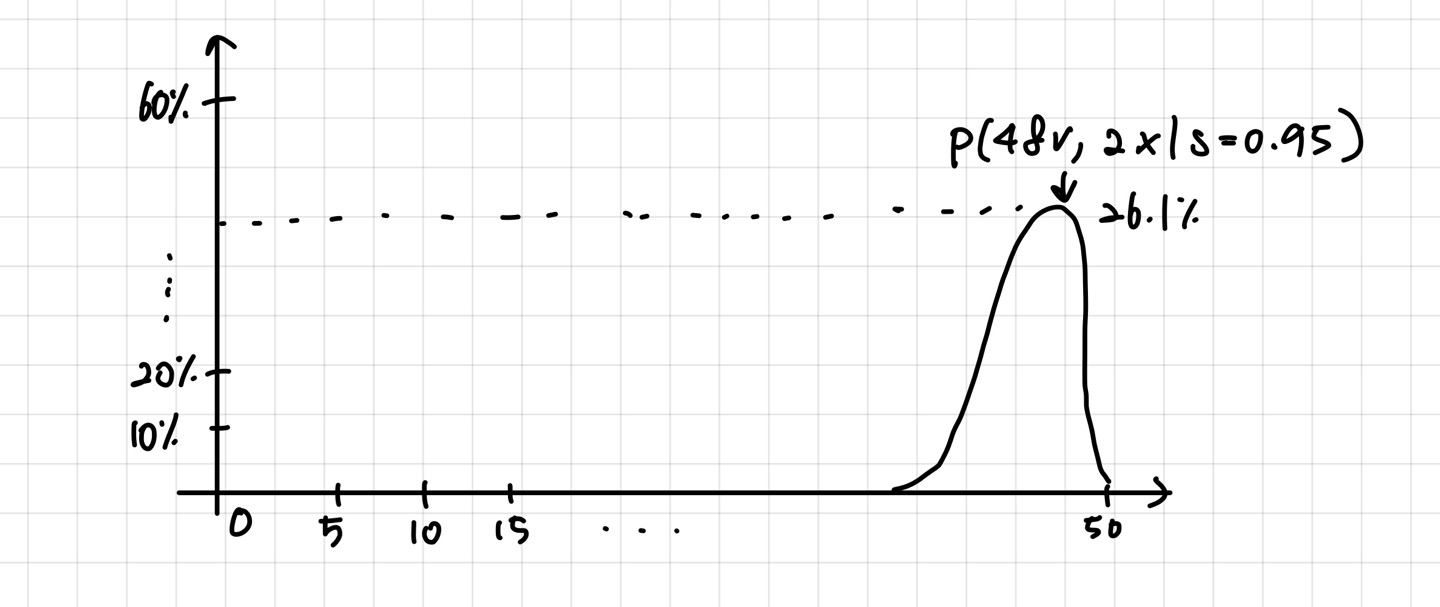
위의 그림과 같이 전체확률에서 48개의 참, 2개의 불만족이 나올 확률은 26%이죠.

이와 같은 분포는 다음과 같은 식으로 구할 수 있습니다. 

50개중에 랜덤으로 48개를 택하고, s가 맞을 확률인 0.95와 아닐 확률 1-0.95에 각각의 개수를 제곱하여 곱해줍니다. 

이때 각각의 리뷰가 서로 영향을 주지 않죠.

즉, 독립적인 사건을 가정으로 합니다.

이렇게 만들어진 분포를 "Binomial Distribution"입니다.

확률론에서 가장 기본적인 분포이죠.

하지만 우리가 알고자하는것은 s가 주어졌을 때의 상황이 아닌,

어떤 데이터가 주어졌을 때 어느 s가 참일 확률이죠.

이는 베이즈 이론을 통해 구할 수 있게 됩니다.

하지만 오늘 우리가 알게 된 것은!!

확률 s가 주어졌을 때, 해당 data가 나올확률입니다.

그럼 뿅~

출처 :

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 

필기본 공유해요 

알아보기 힘들겠지만, 필요하신 분들은 가져다 쓰세요

함께 따라와줘서 고마워요! 

출처:

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 

안녕하세요

호떡입니다.

어느덧, 

벌써 마지막 ㅠㅠ

선형대수 정리가되었네요.

여기까지 제 게시글을 봐주셨다면..

정말 감사합니다...

이해가 안되는 부분도 많을텐데,

저는 정리 개념으로 쓴거라

위의 출처 영상 참고하셔서 공부하는 것도 좋을 것 같습니다.

강의가 별로 안길어서!!

출근길이나 퇴근길에 듣는거 강력추천합니당 

그럼 시작해볼게요~

----------------------------------------------------------------------------------------------------------

오늘은 가장 원론적인 것을 다룰 것입니다.

그래서 도대체 벡터란 무엇인가~~~~~~~~~!!!!!!

잠시 스크롤을 멈추고 잠깐 생각하는 시간을 가져보죠.

3

2

1

...........

다들 답을 결정하셨나요?

그럼 설명 시작하도록 하겠습니다.

저번시간에 배운 

우리는 보통 벡터를 얘기할때,

원점을 중심으로 화살표를 그립니다.

하지만 사실, 벡터는 숫자의 배열로 정의하는 게 가장 정확합니다.

숫자의 나열인 것이죠.

좌표계는 단지 기저벡터를 어떻게 정하냐에 따라 수시로 바뀌는 system입니다.

잠시 이전시간에 배운 개념을 정리해봅시다. 

determinant는 변환이 얼마나 면적을 scailing하는 지를 나타내며,

eigen vector는 변환이 일어나도 span을 벗어나지 않는 벡터인 것이죠.

이것을 어떤 system내에서 정의한 것이냐~!

바로 Linear Transform, 선형변환으로부터 정의된 것에 의해 나온 개념입니다.

도대체 선형대수학의 개념을 어디서 쓸까요?

왜 배우는 걸까요??

다음 예시를 봅시다.

우리가 아주~~~

많이보는 미분입니다.

그리고 선형변환의 성질인 Additivity, scailing과 엮어 생각해보죠.

Additivity의 성질은 선형변환 전 두 벡터를 더한 값과, 선형 변환 후 두 벡터를 더한 것은 같다 라는 뜻입니다.

scailing은 선형변환 전 후 언제든지 스칼라 값을 곱했을 때 결과 값이 같은 것 이죠.

즉, 선형변환은 합과 실수배를 보존한다고 한번에 얘기할 수 있습니다. 

이때, 잘 생각해보면 미분은 저 두 가지 성질을 다 만족합니다. 

식을 보니 이해가 되시나요?

결국 미분은 선형 system이기 때문에, 벡터의 개념을 적용해 선형변환을 마치 우리가 선형대수 풀듯이 풀 수 있습니다. 

결국 우리가 공부했던 선형변환과, 미분은 같은 종류라고 볼 수 있습니다.

그럼 벡터란 무엇일까?

현대에서는 벡터의 정의를 신경쓰지 않습니다.

단지, 이용할 뿐이죠.

조건만 선형이라면,

우리는 선형대수 시스템을 간편하게 이용할 수 있습니다.

WOW~~~

멋진 마무리였네요.

선형대수,

들여다 보니 정말 흥미로운 과목이었습니다.

다음부턴 확률론으로 돌아오도록 할게요 

뿅

출처:

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 

안녕하세요

호떡입니다.

오늘은 고유벡터와 고윳값의 의미를 파헤쳐보도록 하겠습니다.

----------------------------------------------------------------------------------------------------------

고윳값에 대한 것은 아래 식을 통해 많이 접해보셨을 텐데요

바로 대각행렬에 람다를 곱해 determinant를 구하고,

람다값을 찾으면 그거 자체가 고윳 값이 됩니다.

하지만 고유벡터의 정의는 따로 존재하죠.

선형변환을 해도 스케일링만 되고 자신의 span을 벗어나지 않는 벡터들을

우리는 고유벡터라고 부르고, 그 회전에서의 고유벡터,  자신의 span에 남아있는 벡터를 찾을 수 있다면 그것이 바로 회전축이 됩니다.

고유값은  변환 도중 늘어나고 줄어드는 정도의 배수에 불과하죠.

이 의미를 되짚어보며 정리를 해보자면,

결국 그 span은 변하지 않으면서 람다값으로 스케일링한 결과와 같습니다.

하지만 행렬벡터 곱셈과 스칼라 벡터 곱셈은 같지 않죠.

람다값, 고윳값으로 스케일링 한다는 것은

항등행렬 I에 람다를 곱하는 것과 같습니다. 

결국 람다는, 람다 * I로 쓸수 있게되고,

양면으로 넘겨주면 (A-람다*I)v  = 0이 됩니다.

determinant가 0이 되는 것을 찾는 다는 건, 

그 공간의 차원을 낮추는 변환을 찾는 것 입니다. 

결국 det(A-람다*I)=0이 되는 람다값을 계산할 수 있게 되는 것이죠.

최종 정리 식은 다음과 같습니다. 

정말 익숙한 식이지만

이제는 다른 관점으로 이해가 되실거라 생각합니다. 

여기서 고유기저, eigen basis의 의미를 짚고 넘어가도록 하겠습니다.

고유기저란,

기저벡터가 고유벡터가 됨을 뜻합니다.

기저벡터 i,j자체가 고유벡터로 정의되는 것이죠.

이는 대각선 외에 모두 0인 행렬, 대각선 행렬이 A일 경우 해당합니다.

다음은 고윳값을 쉽고 빠르게 구하는 방법이니, 참고하시길 바랍니다.

그럼 뿅~!

출처 : 

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 

안녕하세요

호떡입니다.

바로 시작해볼까요~?

--------------------------------------------------------------------------------------------------------------------------------------

오늘은 "좌표계"의 기저벡터의 변환과 적용에 대해 알아볼 것입니다. 

벡터 3,2 를 생각해보죠.

우리는 3,2를 Basis vector, 기저벡터로 나타낼 수 있습니다.

바로 

3i + 2j 처럼 말이죠.

좌표계 뒷면에 그려지는 Grid는 (저는 복잡해서 못그렸지만 .. ㅠㅠ) 시각적 도움에 불과합니다.

하지만, 어떻게 그리던 원점은 같습니다. 

이때 원점은, 어떤 벡터를 가지고 있던 크기를 0으로 줄였을 때 의미하는 곳 입니다. 

우리가 일반적인 좌표계에서 가지고 있는 기저벡터 i,j 자체를 다른 벡터로 정하면 어떨까요?

우리 좌표계의 basis vector를 바꿔보는 거죠!

바뀐 basis vector의 세계를, 제니퍼의 관점으로 묘사해보도록 하겠습니다. 

만약 제니퍼는 b1, b2를 기저벡터로 정의하였다고 합시다. 

제니퍼가 자신의 관점에서 (-1,2)벡터 (초록색)을 그렸다고 할때, 우리의 좌표계에서는 -1,2가 어떻게 바뀔까요??

바로 선형변환의 식을 통해 구할 수 있습니다. 

제니퍼의 관점인 -1,2에, 제니퍼의 기저벡터를 변환 행렬로 생각하면 됩니다.

우리에게는 -4,1이 되는거죠.

우리의 Grid를 제니퍼의 grid 버전으로 바뀔 수도 있고,

그 반대도 됩니다.

이때 , 앞서와 반대로 변환해주고자 한다면 행렬의 역행렬을 곱해주기만 하면 됩니다. 

우리의 grid에서 정의된 3,2 를 그녀의 grid상에서 표시하려면,

우리는 역행렬을 곱해주기만 하면 됩니다.

제니퍼의 기저벡터는 선형변환 행렬이되어

제니퍼에서 정의된 x,y에 이 행렬을 곱하기만 하면

우리좌표계에서 같은 곳을 나타내는 벡터를 찾는게 가능합니다.

그러면 여러분들이 선형대수를 공부할때 많이 봤을 이 식을 이해할 수 있습니다!

천천히 생각해볼까요?

만약 90도 rotation하는 선형변환 식인 [[ 0 -1 ][ 1 0 ]]을 적용한다고 해보죠.

이때, 이 선형변환 식은 우리 좌표계에서만 90도 회전인 식이죠.

제니퍼의 그리드에 이것을 적용하면 대부분의 경우 90도 회전이 나오지 않습니다.

그렇죠?

하지만 제니퍼의 벡터에 제니퍼의 기저벡터 행렬을 곱해주면, 우리 grid에서 표현할 수 있게됩니다.

그러면 우리의 관점으로 바꿔지게 되고, 여기에는 90도 rotation 선형변환 행렬을 곱할 수 있게되죠.

하지만!

우리는 제니퍼의 그리드에 적용하고 싶은 거잖아요?

결국엔 역으로 다시 제니퍼 기저벡터의 역행렬을 곱해주면,

제니퍼의 그리드에서 90도 회전을 적용할 수 있는거죠.

그럼 이제 이식이 이해 되셨을 것이라 생각합니다. 

그럼 뿅~

출처:

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 

안녕하세요

호떡입니다.

주말에 신나게 ^^ 놀고왔더니

할일이 이따시만큼 쌓여있네요....

놀때 놀고, 공부할때는 공부하는게 좋다 라는 말이

가끔 똑똑한 사람들의 기만처럼 느껴질 때가 있습니다.

공부할 것은 항상 쌓여만가고,

해야할 일도 끊임없이 생기는데

모든걸 끝내고 여유를 가진다는 것은

참 한정적인 상황에서만 존재하는 것 같네요

오늘 갑자기 센치... 하군요 ....^^

빨리 시작해야겠어요!!!

오늘은 저번에 깜빡하고 정리를 못했던 외적의 기하학적 의미를 정리해보려 합니다.

Start !!~ 

---------------------------------------------------------------------------------------------------------------------------------------------------------

너무 오래전에 포스팅해서 다들 까먹으셨을 까봐!!

외적의 식을 한번 상기해봅시다. 

어떤 두 벡터 v와 w를 외적하게 되면 그 정사각형의 넓이와 같은 길이의 새로운 벡터 p가 생겨나는 거였죠.

그리고 식은 간단하게 아래처럼 표현할 수 있습니다.

그럼 여기서 행렬식의 첫번째 열에 i,j,k는 왜 있는 걸까요?

그 자리에 x, y, z를 넣어 생각해봅시다.

1차원 변환을 할 수 있는 1X3 matrix를 한번 생각해보죠

이는 determinant의 정의에 의해 오른쪽 식은 모든 입력벡터 x,y,z에 대해 벡터 v와 w에 정의된 평행육면체가 됩니다.

이때, x,y,z에 좌표계의 기저벡터인 i, j, k가 사용됨으로써 그 계수들이 한 벡터의 좌표로 해석된다는 의미이죠. 

결국, 

스칼라 값과 세가지 기저벡터들의 합으로써 새로운 벡터를 표현할 수 있습니다.

이게바로 외적! 인것이에요

다들 이해되셨나요~? 

오늘은 좀 짧게 준비해봤는데,

이때까지의 개념들을 잘 종합해서 살펴보면 금방 이해할 수 있을 것이라 생각합니다.

그럼 뿅!

출처:

https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab 

안녕하세요

호떡입니다!!

어제 너무너무 바빠서 포스팅을 미뤄버렸네요ㅠㅠ 

갑자기 할일들이 몰려와서..는 아니고 원래 항상 많았어서

시험은 없기때문에 마음은 편하지만 열심히 살고 있습니다 ㅎㅎ

서론이 길었네요

그럼 시작해보겠습니당~!

--------------------------------------------------------------------------------

저번에 외적에 대한 많은 궁금증을 뒤로한 채 포스팅을 마무리했었죠...

오늘은 크래머 공식을 기하학적으로 설명해보려 합니다.

그전에 선형변환의 내적에 대해 잠시 짚고 넘어가도록 하겠습니다.

과연 변환 전 내적과 변환 후 내적은 같을까요? 

다들 멈춰서 한번 생각해봅시다!!!

정답은...

틀립니다!!

변환 후 내적은 다를 수 있습니다.

예시를 들어 설명해보겠습니다.

위 그림이 변환 전, 

아래 그림이 변환 후 라고 생각해보죠.

여러분들 내적의 부호는 어떻게 되는지 기억하시나요?

내적은 같은 방향일 때 양수가 나옵니다.

근데 아래 그림을 보면, 두 벡터의 방향이 다르니까 음수가 나옵니다.

결국 변환 후 내적은 다릅니다.

근데, 변환 후 내적이 같은 특별한 변환도 있습니다.

바로 내적을 보존하는 변환이죠.

바로 직교변환이죠!

바로 늘어짐, 찌그러짐 또는 변형이 없는 단단한 변형이죠.

바로 아래 예시가 그러한 예시입니다.

왼쪽의 행렬은 orthogonal행렬인데요,

여기서 x, y는 위와 같이 구할 수 있습니다.

기억하시죠?

크래머 공식을 이해하기 전에, 위의 그림을 한번 봅시다.

i와 벡터로 이루어진 평행사변형의 넓이는, i의길이 X y로 생각할 수 있습니다.

반대로, 아래 그림은 j의 길이 X x 가 면적이 되죠.

여기까지는 이해 하셨죠?

그럼 여기서 3차원 좌표계를 한번 생각해봅시다.

어쩌피 기존 좌표계의 기저벡터 i,j,k는 길이가 1이니 면적은 1이되고, 평행사변형의 부피는 벡터가 가리키는 길이 그 자체가 됩니다. 즉, 해당 부피는 세번째 좌표인 높이와 같게되죠.

그럼 크래머 공식을 한번 이해해볼까요??

그럼 위의 행렬변환을 한번 생각해보죠.

결국 넓이는 y에서 det A만큼 늘어나게 됩니다.

이것은 detA의 정의를 보면 아시겠죠?

또한 y = area/det(A)가 되고, Area는 변환 후 벡터의 좌표와 행렬의 determinant이기 때문에

결국 y = Area/det(A) 가 성립하게 됩니다.

다시 한번 더 이해를 위해, 반대의 케이스를 봅시다.

위의 그림이 변환전, 그 다음 그림이 변환 후라고 생각해보죠.

변환 전 면적은 그림과 같이 x가 됩니다.

그리고 행렬을 통해 변환하면, 면적은 이전면적의 x에 determinant(A) 값을 곱한 것이 됩니다.

변환 후 면적은 변환 후 벡터와 변환 후 (빨간색 벡터) j벡터의 행렬의 determinant를 구하면 되겠죠

결국 x = Area / detA가 됩니다.

결국 x는 위와 같이 경험할 수 있고, 이것이 바로 크래머 공식입니다.

다들 이해되셨죠~?

그럼 오늘의 포스팅은 여기까지!

행복한 저녁 보내세요