출처:
https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
Essence of linear algebra
A geometric understanding of matrices, determinants, eigen-stuffs and more.
www.youtube.com
안녕하세요
호떡입니다!!

어제 너무너무 바빠서 포스팅을 미뤄버렸네요ㅠㅠ
갑자기 할일들이 몰려와서..는 아니고 원래 항상 많았어서
시험은 없기때문에 마음은 편하지만 열심히 살고 있습니다 ㅎㅎ
서론이 길었네요
그럼 시작해보겠습니당~!
--------------------------------------------------------------------------------
저번에 외적에 대한 많은 궁금증을 뒤로한 채 포스팅을 마무리했었죠...
오늘은 크래머 공식을 기하학적으로 설명해보려 합니다.
그전에 선형변환의 내적에 대해 잠시 짚고 넘어가도록 하겠습니다.
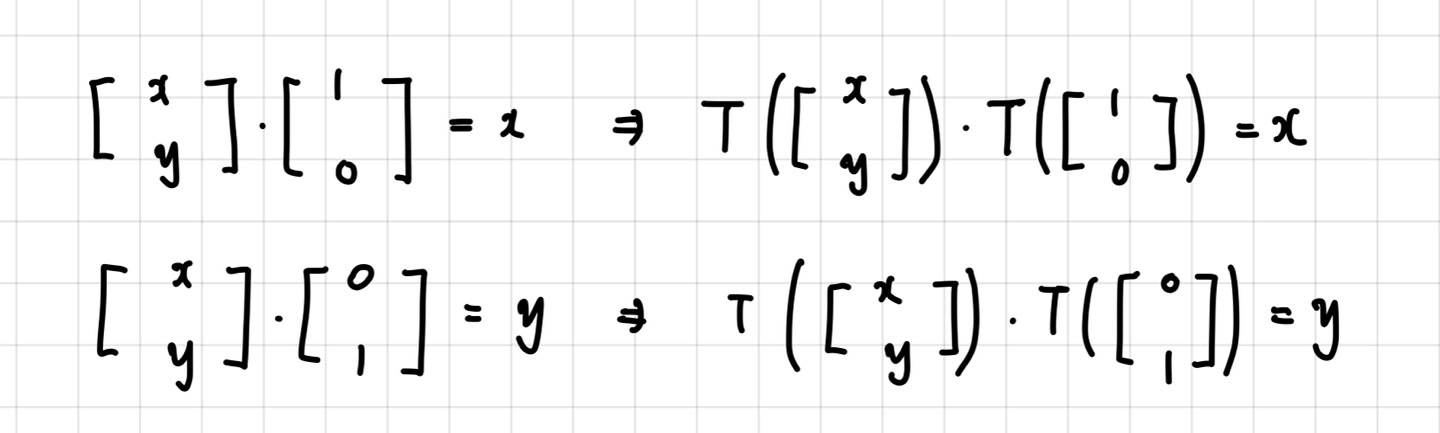
과연 변환 전 내적과 변환 후 내적은 같을까요?
다들 멈춰서 한번 생각해봅시다!!!
정답은...
틀립니다!!
변환 후 내적은 다를 수 있습니다.
예시를 들어 설명해보겠습니다.
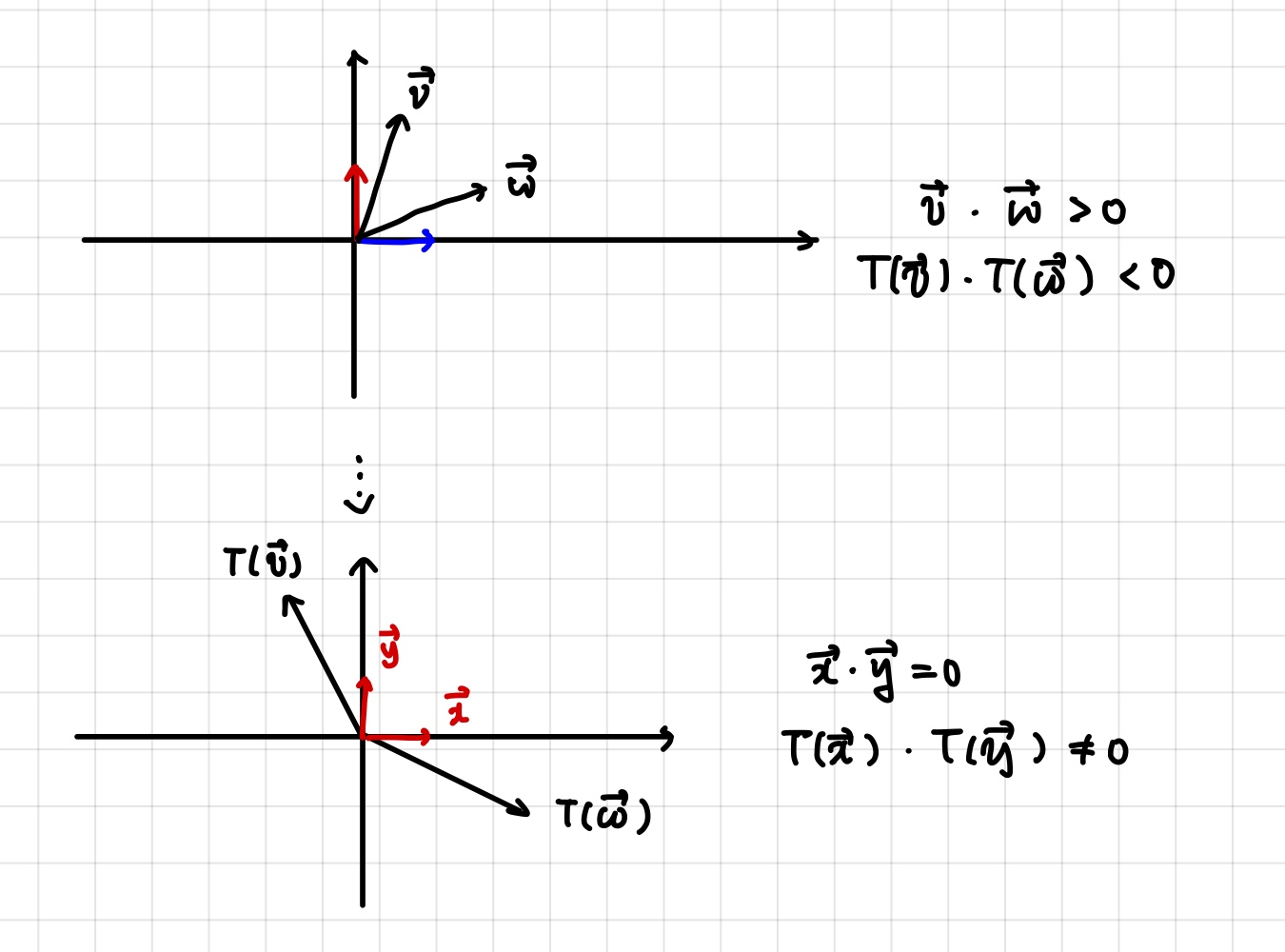
위 그림이 변환 전,
아래 그림이 변환 후 라고 생각해보죠.
여러분들 내적의 부호는 어떻게 되는지 기억하시나요?
내적은 같은 방향일 때 양수가 나옵니다.
근데 아래 그림을 보면, 두 벡터의 방향이 다르니까 음수가 나옵니다.
결국 변환 후 내적은 다릅니다.
근데, 변환 후 내적이 같은 특별한 변환도 있습니다.
바로 내적을 보존하는 변환이죠.

바로 직교변환이죠!
바로 늘어짐, 찌그러짐 또는 변형이 없는 단단한 변형이죠.
바로 아래 예시가 그러한 예시입니다.
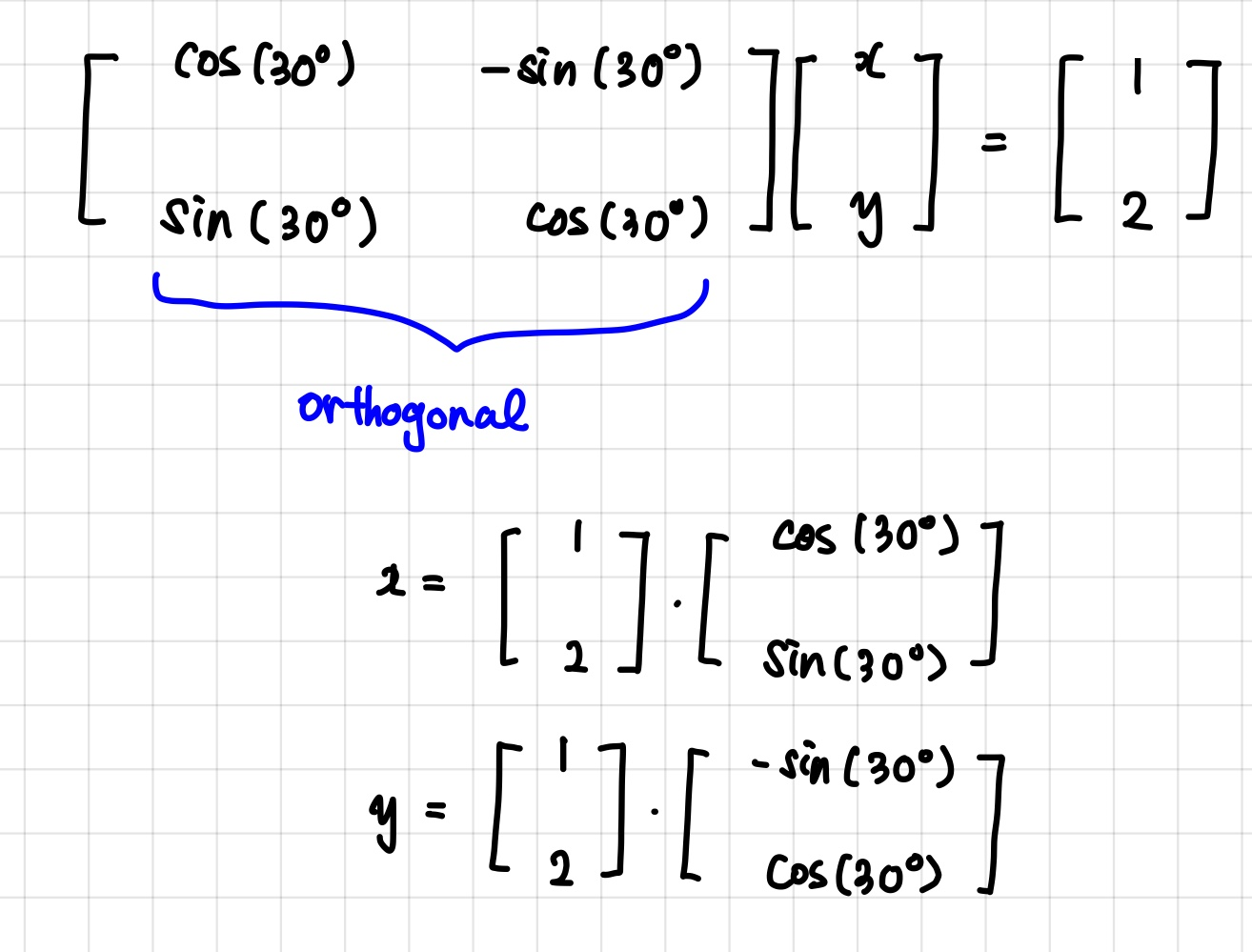
왼쪽의 행렬은 orthogonal행렬인데요,
여기서 x, y는 위와 같이 구할 수 있습니다.
기억하시죠?
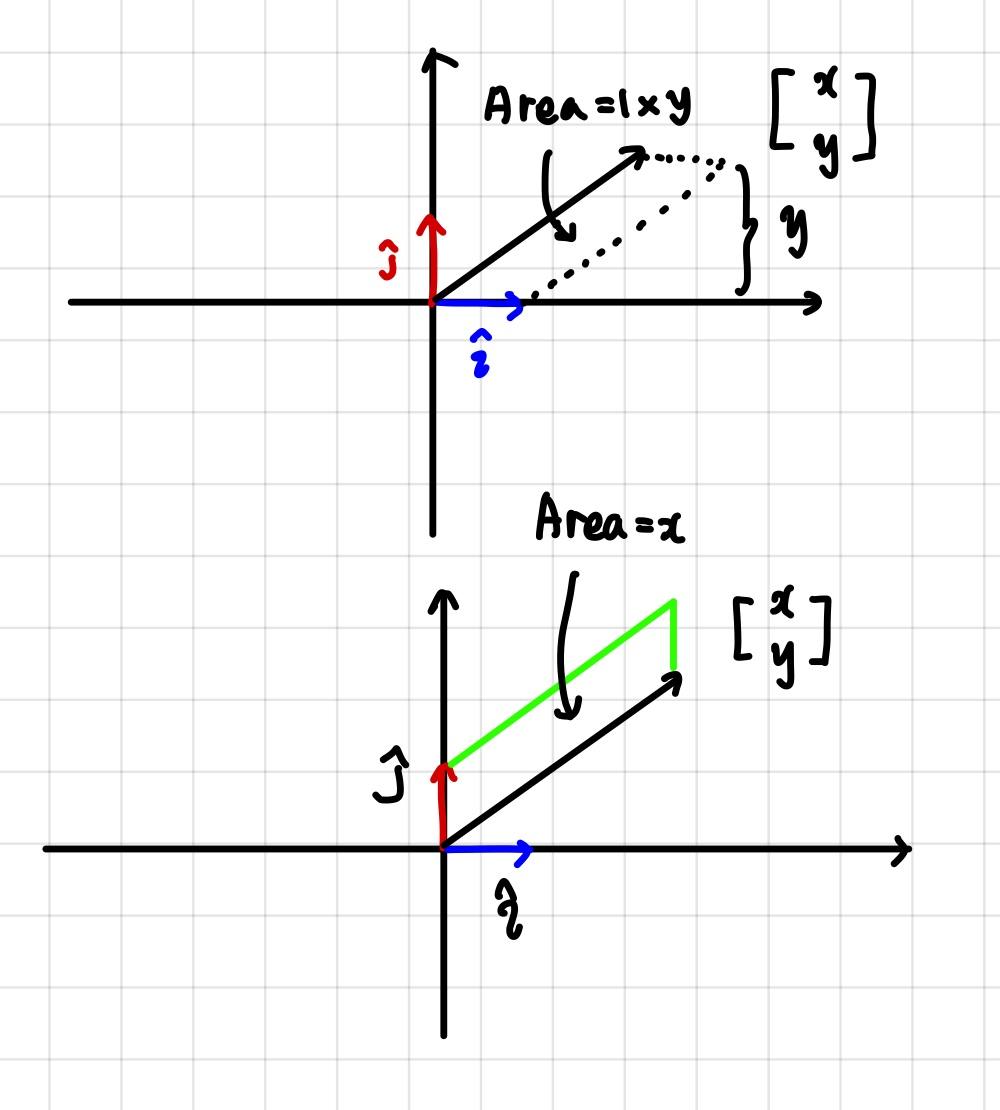
크래머 공식을 이해하기 전에, 위의 그림을 한번 봅시다.
i와 벡터로 이루어진 평행사변형의 넓이는, i의길이 X y로 생각할 수 있습니다.
반대로, 아래 그림은 j의 길이 X x 가 면적이 되죠.
여기까지는 이해 하셨죠?
그럼 여기서 3차원 좌표계를 한번 생각해봅시다.
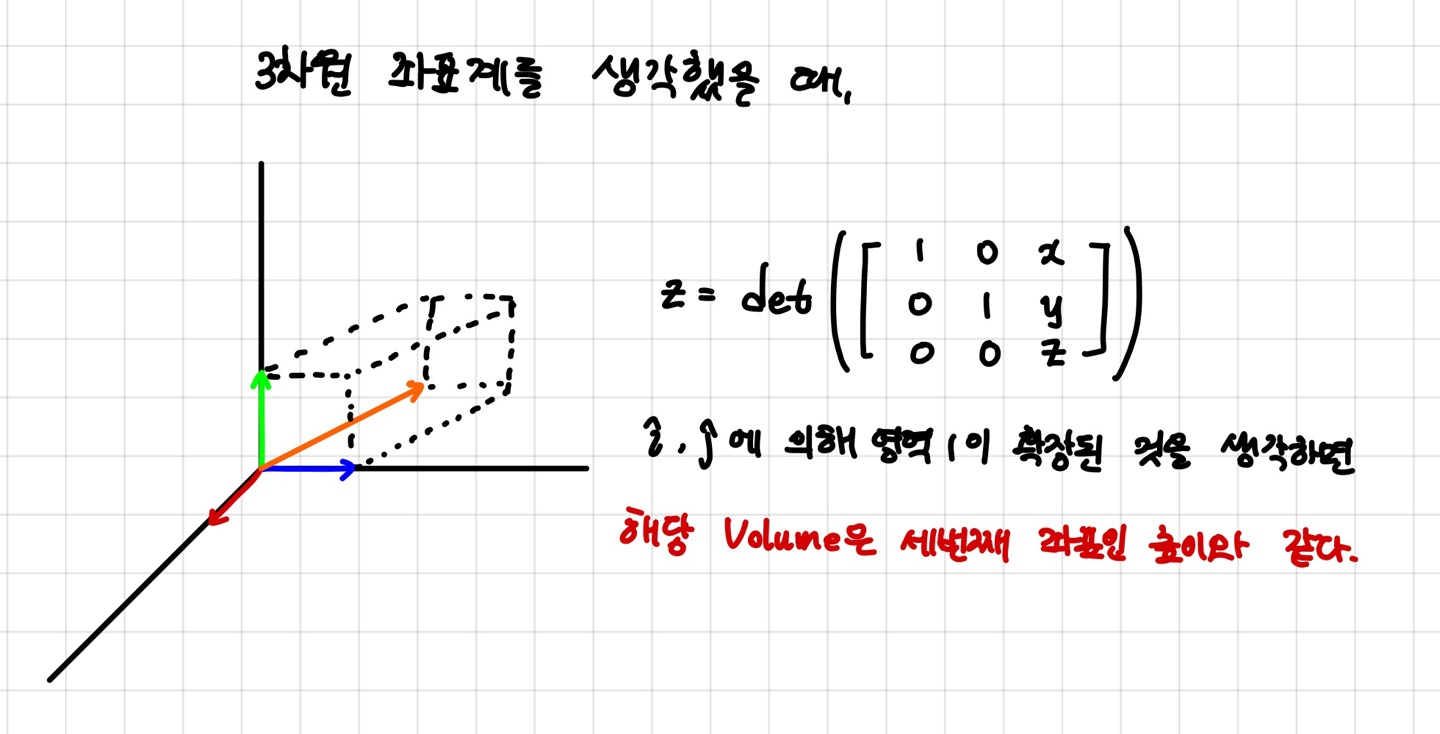
어쩌피 기존 좌표계의 기저벡터 i,j,k는 길이가 1이니 면적은 1이되고, 평행사변형의 부피는 벡터가 가리키는 길이 그 자체가 됩니다. 즉, 해당 부피는 세번째 좌표인 높이와 같게되죠.
그럼 크래머 공식을 한번 이해해볼까요??
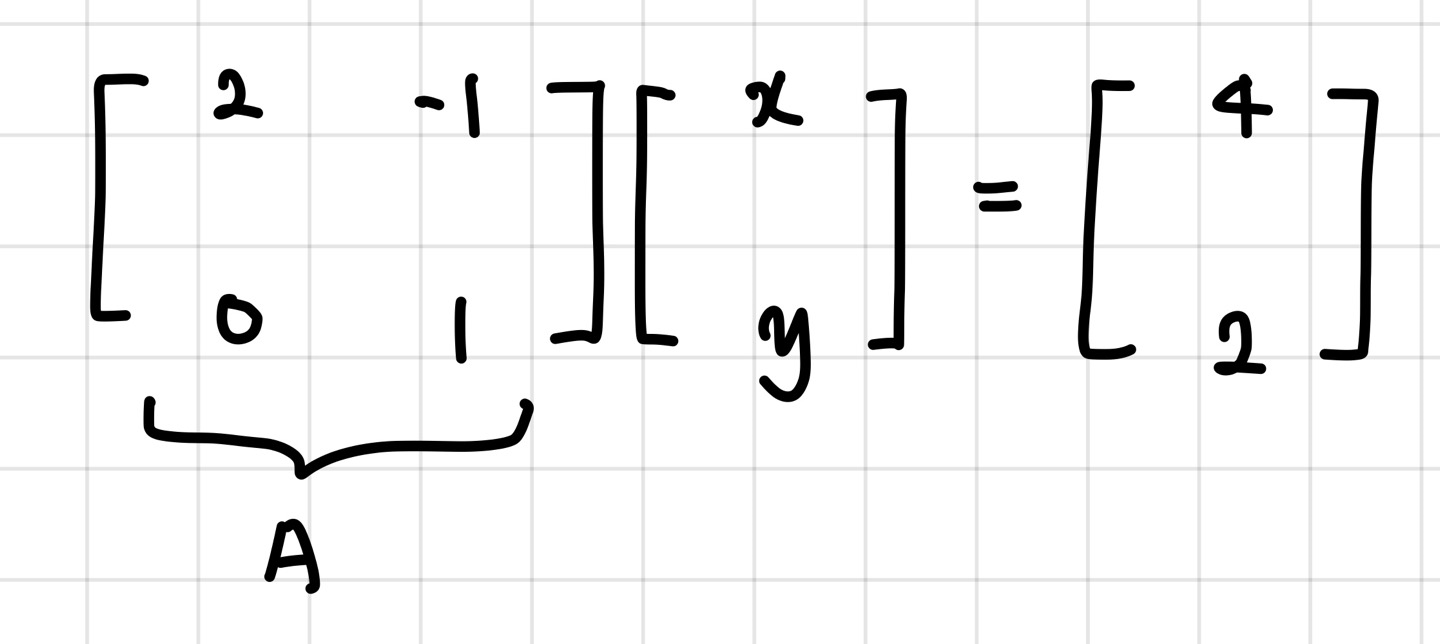
그럼 위의 행렬변환을 한번 생각해보죠.

결국 넓이는 y에서 det A만큼 늘어나게 됩니다.
이것은 detA의 정의를 보면 아시겠죠?
또한 y = area/det(A)가 되고, Area는 변환 후 벡터의 좌표와 행렬의 determinant이기 때문에
결국 y = Area/det(A) 가 성립하게 됩니다.

다시 한번 더 이해를 위해, 반대의 케이스를 봅시다.
위의 그림이 변환전, 그 다음 그림이 변환 후라고 생각해보죠.
변환 전 면적은 그림과 같이 x가 됩니다.
그리고 행렬을 통해 변환하면, 면적은 이전면적의 x에 determinant(A) 값을 곱한 것이 됩니다.
변환 후 면적은 변환 후 벡터와 변환 후 (빨간색 벡터) j벡터의 행렬의 determinant를 구하면 되겠죠
결국 x = Area / detA가 됩니다.
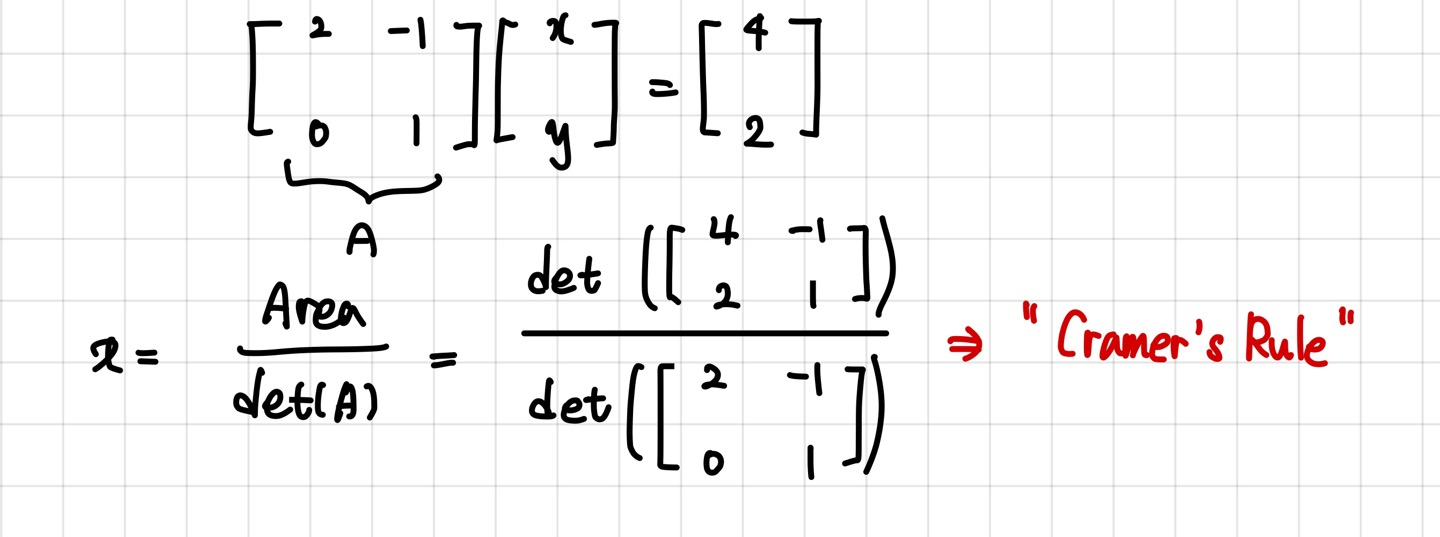
결국 x는 위와 같이 경험할 수 있고, 이것이 바로 크래머 공식입니다.
다들 이해되셨죠~?
그럼 오늘의 포스팅은 여기까지!
행복한 저녁 보내세요

'Linear algebra' 카테고리의 다른 글
| [Linear algebra] Chapter 13: Change of basis (0) | 2022.07.11 |
|---|---|
| [Linear algebra] Chapter 11: Cross product in the light of linear Transforms (0) | 2022.07.11 |
| [Linear algebra] Chapter10: Cross Product (0) | 2022.07.06 |
| [Linear algebra] Chapter9: Dot products and duality (0) | 2022.07.05 |
| [Linear algebra] Chapter8: Nonsquare matrices as transforms between demensions (0) | 2022.07.04 |