출처:
https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
Essence of linear algebra
A geometric understanding of matrices, determinants, eigen-stuffs and more.
www.youtube.com
안녕하세요
호떡입니다.
주말에 신나게 ^^ 놀고왔더니
할일이 이따시만큼 쌓여있네요....
놀때 놀고, 공부할때는 공부하는게 좋다 라는 말이
가끔 똑똑한 사람들의 기만처럼 느껴질 때가 있습니다.
공부할 것은 항상 쌓여만가고,
해야할 일도 끊임없이 생기는데
모든걸 끝내고 여유를 가진다는 것은
참 한정적인 상황에서만 존재하는 것 같네요
오늘 갑자기 센치... 하군요 ....^^
빨리 시작해야겠어요!!!
오늘은 저번에 깜빡하고 정리를 못했던 외적의 기하학적 의미를 정리해보려 합니다.
Start !!~
---------------------------------------------------------------------------------------------------------------------------------------------------------
너무 오래전에 포스팅해서 다들 까먹으셨을 까봐!!
외적의 식을 한번 상기해봅시다.
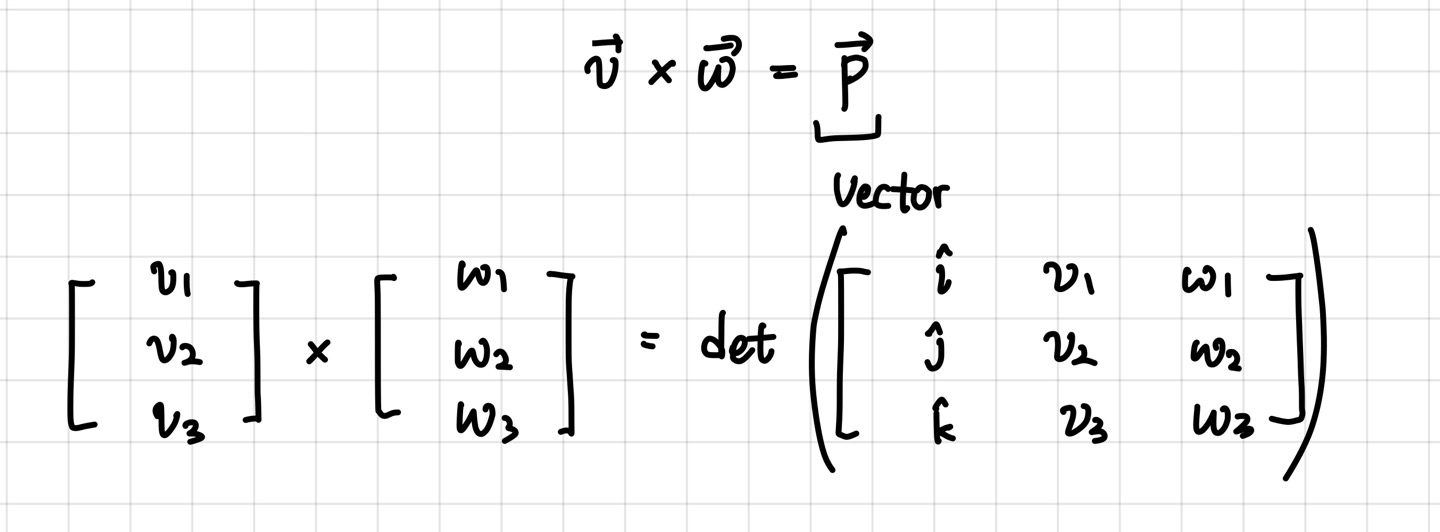
어떤 두 벡터 v와 w를 외적하게 되면 그 정사각형의 넓이와 같은 길이의 새로운 벡터 p가 생겨나는 거였죠.
그리고 식은 간단하게 아래처럼 표현할 수 있습니다.
그럼 여기서 행렬식의 첫번째 열에 i,j,k는 왜 있는 걸까요?
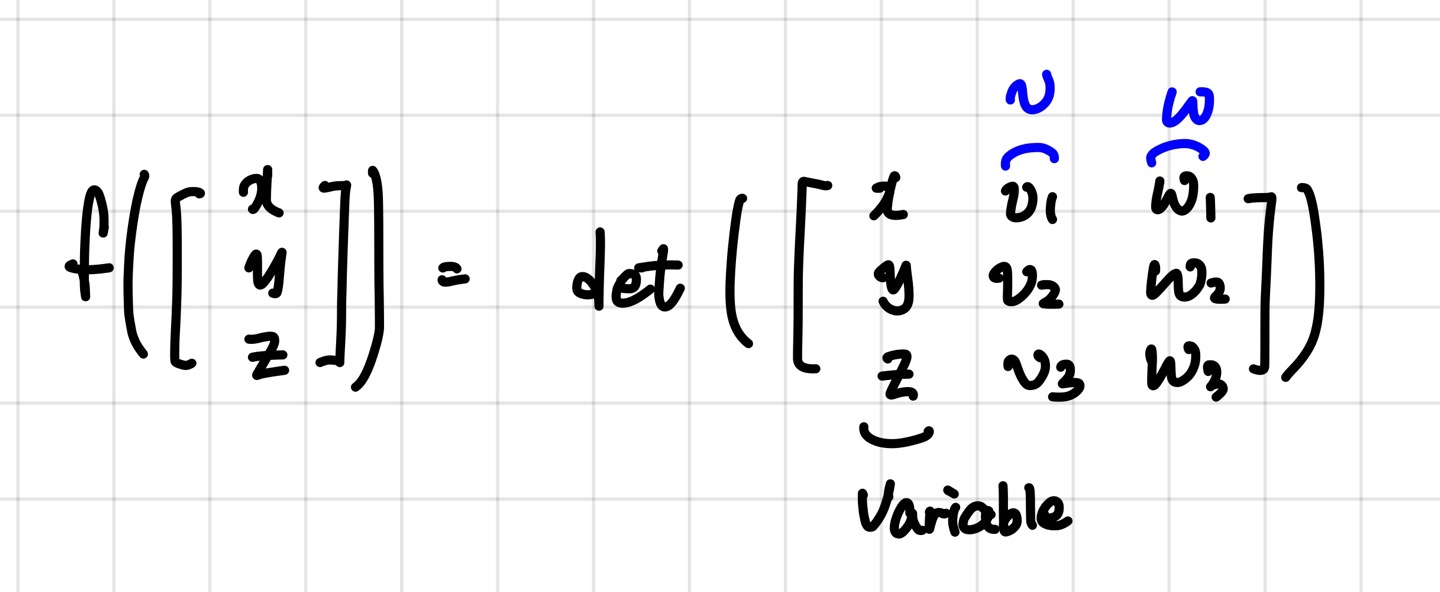
그 자리에 x, y, z를 넣어 생각해봅시다.

1차원 변환을 할 수 있는 1X3 matrix를 한번 생각해보죠
이는 determinant의 정의에 의해 오른쪽 식은 모든 입력벡터 x,y,z에 대해 벡터 v와 w에 정의된 평행육면체가 됩니다.
이때, x,y,z에 좌표계의 기저벡터인 i, j, k가 사용됨으로써 그 계수들이 한 벡터의 좌표로 해석된다는 의미이죠.
결국,
스칼라 값과 세가지 기저벡터들의 합으로써 새로운 벡터를 표현할 수 있습니다.
이게바로 외적! 인것이에요
다들 이해되셨나요~?
오늘은 좀 짧게 준비해봤는데,
이때까지의 개념들을 잘 종합해서 살펴보면 금방 이해할 수 있을 것이라 생각합니다.
그럼 뿅!
'Linear algebra' 카테고리의 다른 글
| [Linear algebra] Chapter 14-15, Eigenvectors and Eigenvalues (0) | 2022.07.11 |
|---|---|
| [Linear algebra] Chapter 13: Change of basis (0) | 2022.07.11 |
| [Linear algebra] Chapter 12: Let's understand Kramer's formula geometrically (0) | 2022.07.08 |
| [Linear algebra] Chapter10: Cross Product (0) | 2022.07.06 |
| [Linear algebra] Chapter9: Dot products and duality (0) | 2022.07.05 |