안녕하세요!
자연어 처리에서 핵심 역할을 했었던, RNN과 이후 RNN을 기반으로 파생된 모델인 LSTM과 GRU에 대해 포스팅해보겠습니다.
Recurrent Neural Network (RNN)
RNN: Background
- 시계열 데이터를 처리하기에 좋은 네트워크
- RNN의 기본 전제는 sequence data의 각 요소가 서로 연관성을 가진 다는 것,
- CNN 이 이미지 구역별로 같은 weight를 공유한다면, 시간 별로 같은 weight를 공유한다.
- 기존의 신경망들 (DNN) 은 은닉층에서 activation function을 지나 출력됨 => Feed Forward Neural Network
- But 시계열 데이터는 과거의 상태가 현재 상태에 영향을 미치며, 최종적으로는 Output에 영향을 미침.
- 따라서 시계열 데이터를 처리하기 위해, RNN에서는 현재 시간의 상태 ($ x_t $) 가 이전 시간의 상태($ x_{t-1}$ 와, 현재의 입력 ($ u_{t}$) 에 관련이 있다고 가정함.
- 그럼 다음과 같은 수식을 정의할 수 있음.
- $x_t = f(x_{t-1}, u_t)$
$y_t = h(x_t)$
Neural Network setting으로 함수 근사
- $x_t = \sigma (W_{xx}x_{t-1} + W_{xu}u_t + b_x)$
$y_t = \sigma (W_{yx}x_t + b_y)$ - RNN (Recurrent Neural Network) 는 은닉층의 노드에서 activation function을 통해 나온 결과값을 출력층 방향으로 보내면서, 은닉층 노드의 다음 계산의 입력으로 보냄.
이러한 RNN은 대표적으로 두 가지 그림을 통해 표현할 수 있음. (bias는 생략)
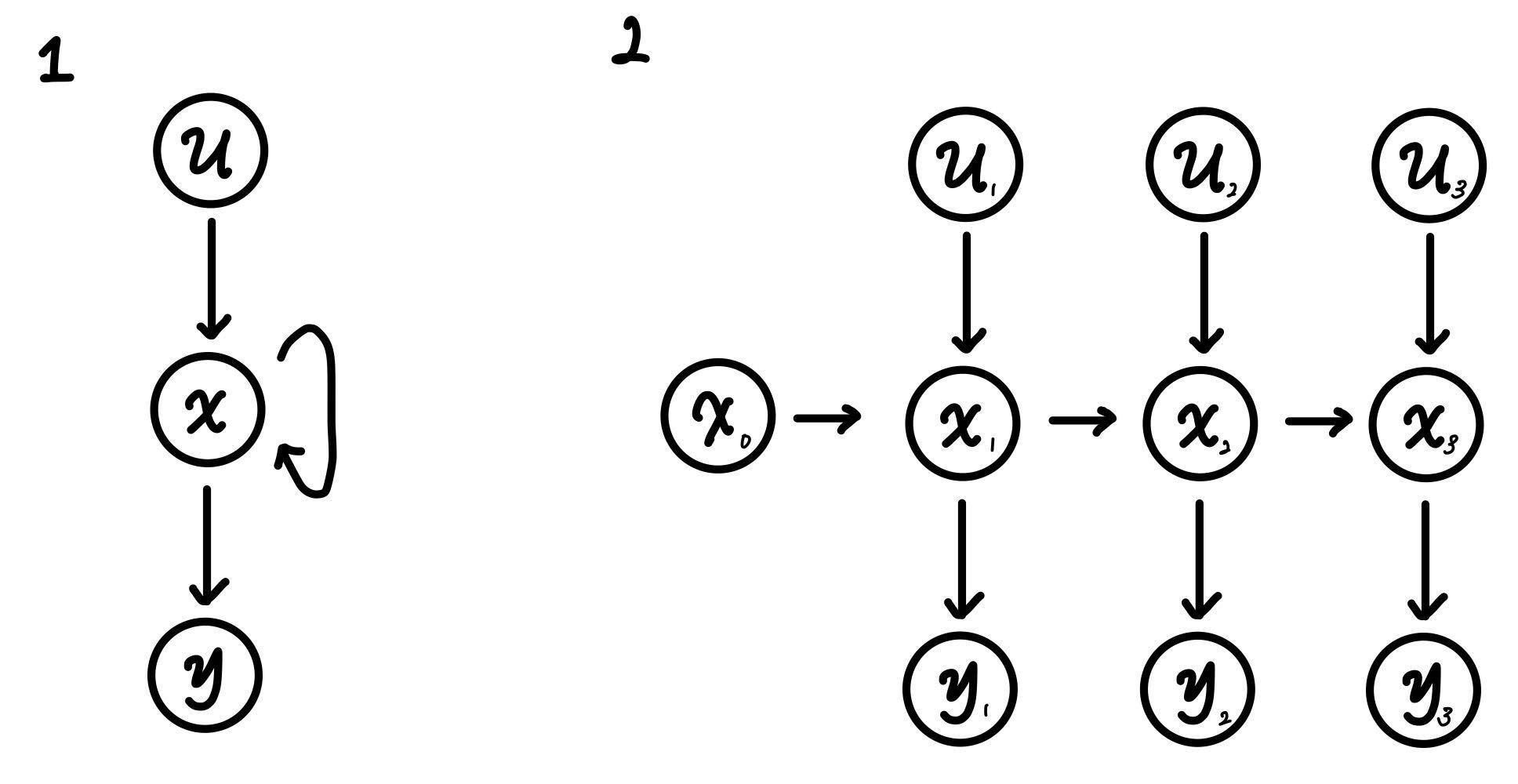
- 각각의 노드는 벡터 형태임.
- 1번과 2번의 그림을 보면 알 수 있듯이, self feedback loop가 존재하는 것을 볼 수 있음. 그리고 $x_t$ 이전 까지의 상태와, 이전까지의 입력을 대표할 수 있는 압축본이라고 할 수 있다. 이러한 hidden state $x$를 셀(cell)이라고 하며, 이전의 값을 기억하는 메모리 역할을 수행하여 메모리 셀 or RNN 셀 이라고 표현한다.
우리가 알기 익숙한 형태로 시각화를 해보자면,

RNN: Problem Types
RNN은 입력과 출력의 길이를 다르게 설계할 수 있어 아래와 같은 3가지 task 로 나눌 수 있음.
- Many-to-many (번역)
- Many-to-one (예측): sentiment classification (입력 문서가 긍정 or 부정), spam detection
- One-to-many (생성): Image captioning (사진의 제목 생성하기)
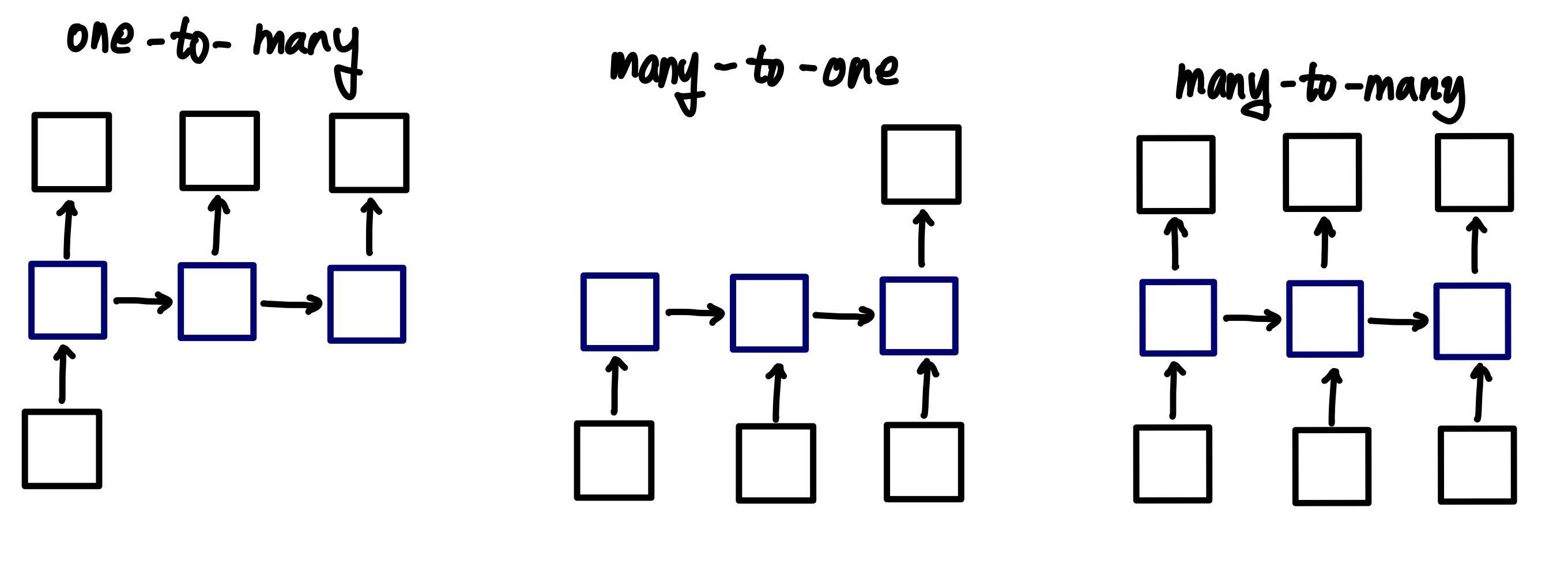
RNN: Training
RNN의 학습은 backpropagation의 확장형인 BPTT(Back Propagation Through Time)를 사용함
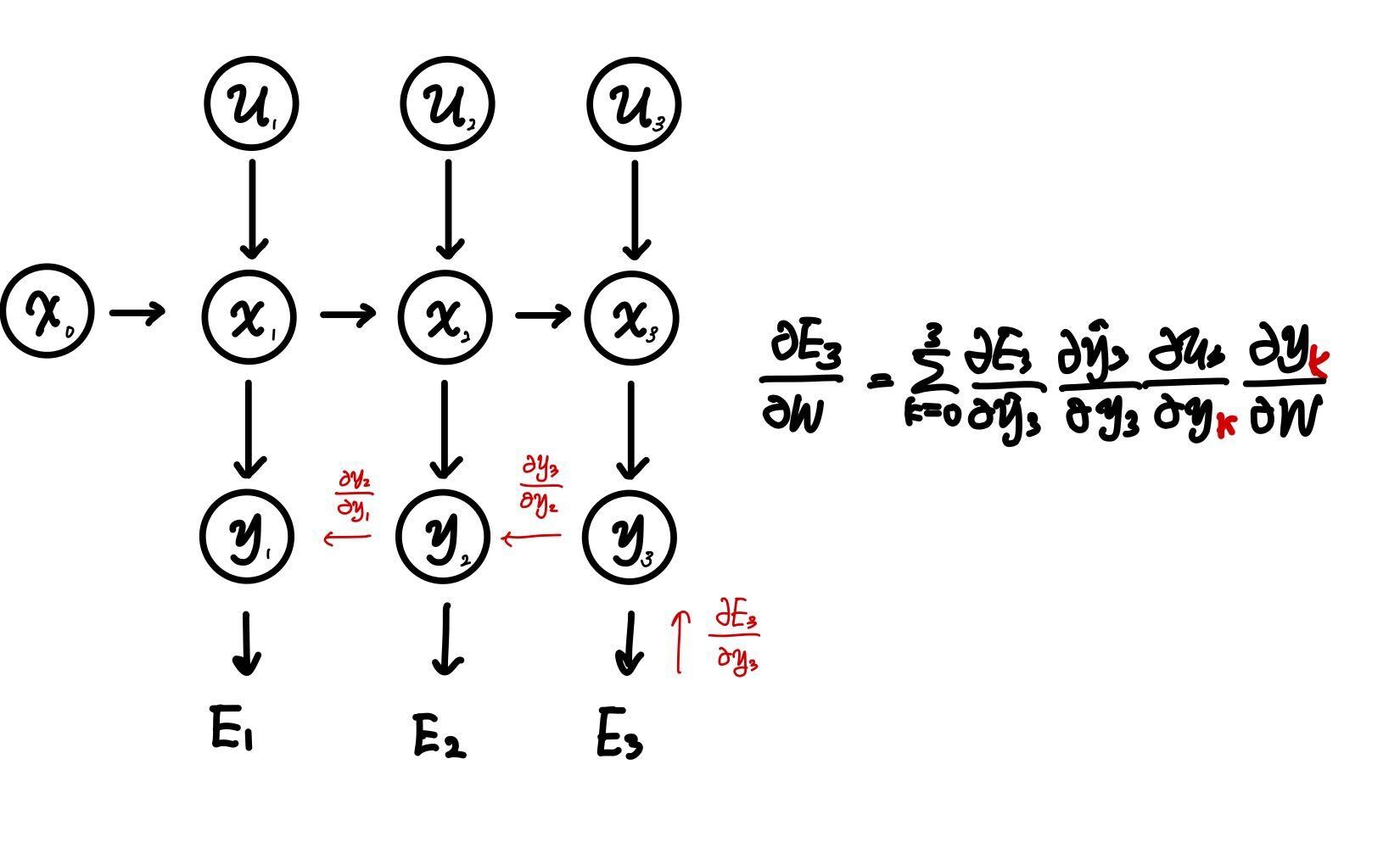
- 가중치 W가 모든 시점에서 메모리 셀의 출력($y$)를 구할 때 사용되었기 때문에 0에서 k까지 계산하여 합하는 것임.
- 이러한 Training 때문에, 전파가 길어질 수록 Gradient Exploding or Gradient Vanishing 현상이 발생함. (정보량의 손실)
- Gradient Exploding => Gradient clipping (gradient가 일정 threshold가 넘어가면, clipping 해줌)을 해 줄 수 있음.
- Gradient Vanishing => 학습 도중 파악하기 어려움. 만약 loss값이 0 이라면 학습이 종료된 것인지, 아니면 Vanishing gradient 인지 모름. 따라서 다른 네트워크 구조를 사용하는 것이 편함
- 따라서 RNN은 긴 의존기간의 문제를 어려워함.
ex, The clouds are in the sky => sky를 맞추기 위해서는 이 문장만 봐도 해결 가능함. I grew up in France ... I speak fluent French => French 를 맞추고 싶다면 앞의 문맥부터 참고 해야함.
아래의 경우는 필요한 정보를 얻기 위해 시간 격차가 굉장히 커지기 때문에, 학습하는 정보를 계속 이어나가기 힘들다.
==> 이를 해결하는 네트워크 구조 **Gated RNNs: LSTM/GRU**
Long short-term memory: LSTM
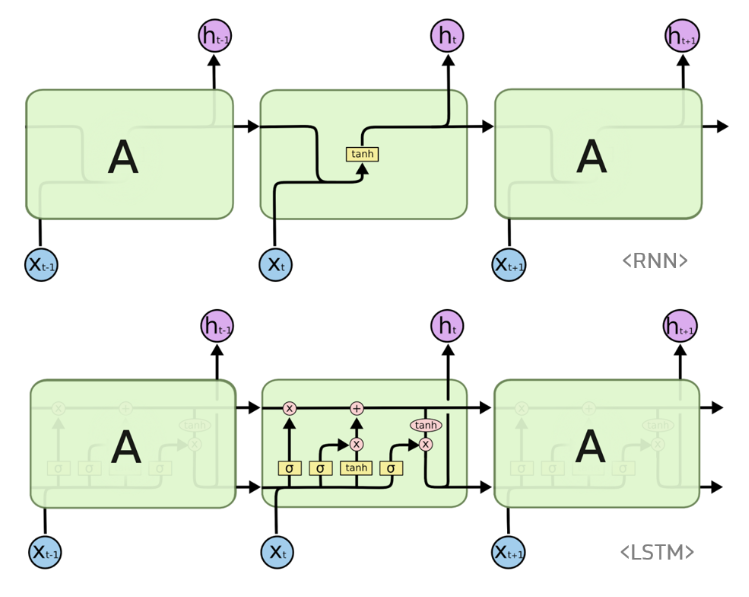
출처:http://colah.github.io/posts/2015-08-Understanding-LSTMs/
앞서 제시된 RNN의 긴 의존 기간의 문제를 피하기 위해 설계되었음.
- hidden state 만이 아니라 cell state 라는 역할이 있으며 Forget gate, Input gate, Output gate를 통해 계산이 이루어짐.
- Gradient flow를 제어할 수 있는 "밸브" 역할을 수행함.
- State space의 입력($x$), 상태($h$), 출력($y$) 구조는 동일함.
- 4개의 Unit을 가지고 있음.
1) Forget gate
2) Input gate
3) Output gate
4) Cell
Gate의 이름에서 알 수 있듯이 어떤 정보를 잊을지 기억할지를 선택해 long term과 short term에 대한 정보를 고려함.
Cell state

- Hidden state와 마찬가지로 이전 시점의 cell state를 다음 시점으로 넘겨줌.
- Cell state의 주 역할은 gate들과 함께 작용해 정보를 선택적으로 활용
- Cell state의 업데이트는 각 gate의 결과를 더함으로서 진행됨.
Gate
- 1), 3), 4)이 gate라고 할 수 있음.
- 세 개의 gate 모두 활성화 함수로 시그모이드 적용 => $\sigma$
- gate는 cell state와 함께 정보를 선택적으로 활용할 수 있도록 함.
1) Forget gate layer

- 과거 정보를 얼마나 잊을 것인지/기억할 것인지 결정하는 단계
- 전 시점의 hidden state $h$와 현재 입력 $x$에 대해 연산을 진행하고, $\sigma$함수 사용 함.
- 이 값이 0에 가까울 수록 정보를 잊은 것이며, 1에 가까울 수록 정보를 기억하는 것임.
- 연산의 결과인 $f_t$는 과거 정보에 관해 얼마나 잊었는지, 기억하는지를 가지고 있는 값임.
2) Input gate layer
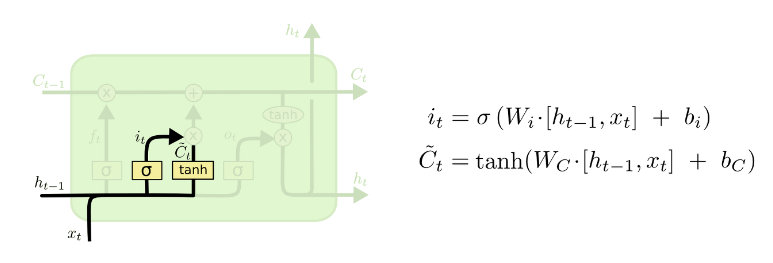
- 새로운 정보 중 어떤것을 cell state에 저장할 것인지?
- forget gate 와 동일한 기능으로 $i_t$는 현재의 정보를 기억할 것인지/기억하지 않을 것인지를 결정함.
- 이후 $h_{t-1}$ $x_t$는 tanh 함수에 들어가 출력값으로 반환되어 hadamarad product()가 되고, 새로운 후보 값인 $C_t$를 만들어 cell state에 더해짐.
3) Cell state update

- 과거 state인 $C_{t-1}$을 업데이트 해서 새로운 cell state인 $C_t$를 만듦. 이때 forget gate에서 잊어야 하는 이전 상태의 정보를 잊어버리고, 현재의 input값의 반영 값을 포함해서 업데이트 해줌.
4) Output gate layer

- 시그모이드 레이어에 $x_{t}$와 $h_{t-1}$이 들어가 0~1사이의 값을 출력하고, 이 값은 cell state의 어느 부분을 output으로 내보낼 지 결정함. 이후 cell state가 tanh에 들어가 나온 출력값과 output gate에서 나온 값이 곱해져 $h_t$가 출력됨. 이 $h_t$는 출력값으로 나가가기도 하며, 다음 state의 input으로 들어감.
Gated Recurrent Unit: GRU

- GRU는 기존 LSTM의 구조를 조금 더 간단하게 개선한 모델임.
- LSTM보다 학습 속도가 빠르지만, 여러 평가에서 LSTM과 비슷한 성능을 보인다고 알려져 있음.
- 데이터 양이 적을 때는 매개변수의 양이 적은 GRU가 더 좋으며, 데이터 양이 많다면 LSTM이 더 좋다고 알려져 있음.
- LSTM의 forget gate, input gate, output gate 를 reset gate, update gate 2개의 gate만을 사용함. 그리고 cell state, hidden state를 하나의 hidden state로 표현함.
1) Reset gate ($r(t)$) : 이전 상태를 얼마나 반영할 지
- 이전 시점의 hidden state, 현 시점의 입력값을 sigmoid에 통과해 이전 hidden state값을 얼마나 활용할 것인지 결정 식(2).
- (3)식에 다시 활용하여 이전 time point의 hidden state에 reset gate를 곱하여 사용함.
2) Update gate ($z(t)$) : 과거와 현재의 정보를 각각 얼마나 반영할 지에 대한 비율 ==> 삭제 게이트와 입력 게이트의 역할을 수행함.
- 과거와 현재의 정보를 각각 얼마나 반영할 지에 대한 비율을 구함.
- 식 (1)을 통한 결과인 $z$는 현재 정보를 얼마나 사용할 지를 반영, $1-z$는 과거 정보를 얼마나 사용할 지에 대해 반영함. 전자는 LSTM의 Input gate, 이후를 forget gate라고 생각할 수 있음.
- 최종적으로는 (4) 식을 통해 현 시점의 hidden state 값을 구할 수 있음.
- GRU 셀은 output gate가 없어 hidden vector $h_t$가 타임 스텝마다 출력되고, 이전 상태의 $h_{t-1}$의 어느 부분이 출력될 지 제어하는 gate controller인 $r_t$가 있는 것임
'Deep-Learning' 카테고리의 다른 글
| [Hugging face PEFT] AdaLora Config, get_peft_model을 이용하여 원하는 pretrained layer만 적용하기 (0) | 2024.04.11 |
|---|---|
| Diffusion Counterfactual explanations (0) | 2023.05.06 |
| [GAN] GAN 및 DCGAN 개념설명 (0) | 2023.01.15 |