출처:
https://www.youtube.com/watch?v=8idr1WZ1A7Q&t=5s
안녕하세요
호떡입니다.
좋은 오후네요.
오늘 자랑 하나 하자면,,
잠을 12시간이나 잤습니다!
오히려 잠을 더 자니 멍한 기운이 드는 군요.
다들 기운 차리시고 오늘의 포스팅 시작하도록 하겠습니다.
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
Probabilities of probabilities Part 1.
여러분은 이번에 휴대폰을 사려고 합니다.
아이폰 13 mini, 아이폰 13, 아이폰 13 pro 중에 고민중이죠.
그리고 각각 제품의 후기를 보게 됩니다.
아이폰 13 mini의 후기는 10개의, 100%의 만족률이었습니다.
아이폰 13은 50개의 리뷰, 96%의 만족률이죠.
아이폰 13 pro 는 200개의 리뷰, 93%의 만족률이었습니다.
그럼 여러분은 단순히 리뷰만 가지고 어떤 것을 사야할지 판단할때,
무엇을 사야 할까요?

확률로만 따지자면 아이폰 13미니를 사는게 최선의 방법일 겁니다. (사실 제 폰이 아이폰 13 mini ㅎㅎ)
그렇지만, 10건의 리뷰밖에 존재하지 않죠.
내가 저 물건을 샀을 때, 만족할 확률을 알아야하는데..
이는 어떻게 알 수 있을 까요?
바로
리뷰가 더 있는듯 생각하면 됩니다.
예를들어 리뷰가 2개 더 있다고 생각해보죠.
그리고 하나는 만족, 하나는 불만족이라고 가정합니다.
아래 그림처럼 말이죠.

원래는 10개중에 10개의 리뷰 모두 100%였다면,
여기서는 12개의 리뷰가 있고 1개의 리뷰가 불만족이니
총확률은 11/12 = 91.7%가 됩니다.
이런식으로 모두 계산해보면,
아이폰 13 mini ==> 91.7% (내가 샀을 때 만족할 확률)
아이폰 13 ==> 49/52 == 94.2%
아이폰 13 pro ==> 187/202 = 92.5%
즉, 내가 샀을 때 만족도가 제일 높은 제품은 아이폰 13입니다!
이런식으로 계산하는 것을 라플라스의 성공법칙이라고 하죠.
자, 그럼 다른 경우를 생각해봅시다.
만족할 확률 s=0.95 가 주어졌을 때,
48개의 리뷰가 만족이고, 2건의 리뷰가 불만족일 확률은 어떻게 될까요?
여러 번의 시뮬레이션을 돌려보고, 아래와 같은 분포가 나왔다고 가정해보죠.
바로 확률의 확률입니다.
만족할 확률이 주어졌을 때, 해당 확률(데이터)가 나올 확률이죠.
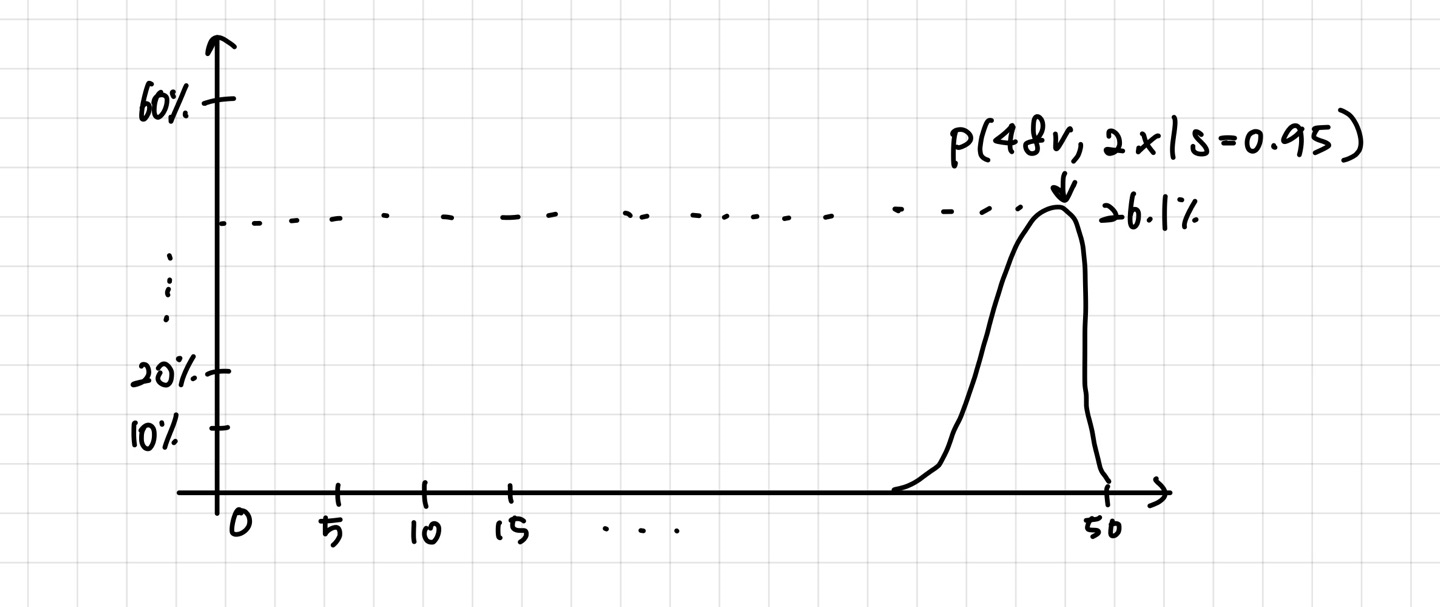
위의 그림과 같이 전체확률에서 48개의 참, 2개의 불만족이 나올 확률은 26%이죠.
이와 같은 분포는 다음과 같은 식으로 구할 수 있습니다.

50개중에 랜덤으로 48개를 택하고, s가 맞을 확률인 0.95와 아닐 확률 1-0.95에 각각의 개수를 제곱하여 곱해줍니다.
이때 각각의 리뷰가 서로 영향을 주지 않죠.
즉, 독립적인 사건을 가정으로 합니다.
이렇게 만들어진 분포를 "Binomial Distribution"입니다.
확률론에서 가장 기본적인 분포이죠.

하지만 우리가 알고자하는것은 s가 주어졌을 때의 상황이 아닌,
어떤 데이터가 주어졌을 때 어느 s가 참일 확률이죠.
이는 베이즈 이론을 통해 구할 수 있게 됩니다.
하지만 오늘 우리가 알게 된 것은!!
확률 s가 주어졌을 때, 해당 data가 나올확률입니다.
그럼 뿅~
'Probability theory' 카테고리의 다른 글
| 조건부 확률이란? (0) | 2023.02.06 |
|---|---|
| 베르누이 분포 / 이항 분포 / 카테고리 분포 / 다항 분포 / 가우시안 정규 분포 / T 분포 / 카이제곱 분포 / F 분포 / 베타 분포 / 감마 분포 / 디리클레 분포 (0) | 2023.02.06 |
| 신뢰 구간(Confidence Interval;CI)란? (0) | 2023.02.06 |
| 샘플링(Sampling)과 리샘플링(Resampling) (0) | 2023.01.15 |